Question

4．已知：如图，AB为⊙O的直径，G为AB上一点，过G作弦CE⊥AB，在$\widehat{BC}$上取一点D，分别作直线CD、ED，交直线AB于点F、M，分别连结OE，CO，CM．
（1）若G为OA的中点．
①∠COA=60°，∠FDM=120°；
②求证：FD•OM=DM•CO．
（2）如图，若G为半径OB上任意一点（不与点O、B重合），过G作弦CE⊥AB，点D在$\widehat{BC}$上，仍作直线CD、ED，分别交直线AB于点F、M，分别连结OE，CO，CM．
①依题意补全图形；
②此时仍有FD•OM=DM•CO成立．请写出证明FD•OM=DM•CO的思路．（不写出证明过程）

Answer 1

分析 （1）①由于CG⊥OA，根据垂径定理可得出，弧CA=弧AE，那么根据圆周角定理可得出∠CDE=∠COA，在Rt△COG中，可根据OG是半径的一半得出∠AOC是60°，那么就能得出∠FDM=180°-∠CDE=120°；②由直径AB⊥CE，根据垂径定理得出AB垂直平分CE，由线段垂直平分线的性质得到MC=ME，则∠CMA=∠EMA，∠FMD=∠CMA，然后根据相似三角形的想尽快得到结论；
（2）①根据题意作出图形即可；②可按（1）的方法得出∠DMF=∠CMO，关键是再找出一组对应角相等，还是用垂径定理来求，根据垂径定理我们可得出弧AC=弧AE，那么∠AOC=∠EDC，根据等角的余角相等即可得出∠COM=∠FDM，由此可证出两三角形相似．

解答 解：（1）①∵OA、OC都是⊙O的半径，且G为OA的中点，
∴在Rt△OCG中，cos∠COG=$\frac{1}{2}$，
∴∠COG=60°，即∠COA=60°；
∵$\widehat{AC}$=$\widehat{AE}$=$\frac{1}{2}$$\widehat{CE}$，
∴∠EDC=∠COA=60°，
∴∠EDF=120°，即∠FDM=120°；
故答案为：60，120；
②∵直径AB⊥CE，
∴AB平分CE，即AB垂直平分CE，
∴MC=ME，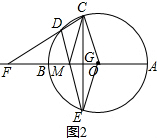
∴∠CMA=∠EMA，
又∵∠FMD=∠EMA，
∴∠FMD=∠CMA，
∵∠FDM=∠COM=120°，
∴△FDM∽△COM，
∴$\frac{DF}{OC}=\frac{DM}{OM}$，
∴FD•OM=DM•CO；

（2）①如图所示；
②结论仍成立．
∵∠EDC的度数=$\frac{1}{2}$$\widehat{CAE}$的度数=$\widehat{AC}$的度数=∠COA的度数，
∴∠FDM=180°-∠COA=∠COM，
∵AB为直径，
∴CE⊥AB，
在Rt△CGM和Rt△EGM中，
$\left\{\begin{array}{l}{GM=GN}\\{∠CGM=∠GM}\\{CG=EG}\end{array}\right.$
∴Rt△CGM≌Rt△EGM（SAS）
∴∠GMC=∠GME，
∵∠FMD=∠EMG，
∴∠FMD=∠CMG，
∴△FDM∽△COM，
∴$\frac{DF}{OC}=\frac{DM}{OM}$，
∴FD•OM=DM•CO．

点评 本题主要考查了圆周角定理，垂径定理，全等三角形和相似三角形的判定及性质等知识点，根据垂径定理得出角相等是解题的关键．