
【题目】某牛奶厂在一条南北走向的大街上设有O,A,B,C四家特约经销店.A店位于O店的南面3千米处;B店位于O店的北面1千米处,C店在O店的北面2千米处.
(1)请以O为原点,向北的方向为正方向,1个单位长度表示1千米,画一条数轴,你能在数轴上分别表示出O,A,B,C的位置吗?
(2)牛奶厂的送货车从O店出发,要把一车牛奶分别送到A,B,C三家经销店,那么送货车走的最短路程是多少千米?
【答案】(1)能,图见解析;(2)送货车走的最短路程是7千米
【解析】
(1)根据题意以O为原点,向北的方向为正方向,1个单位长度表示1千米可画出数轴, 再根据A店位于O店的南面3千米处,可确定A位于O点左边距离原点O 3个单位,即表示-3,B店位于O店的北面1千米处,可确定点B位于点O右边距离原点1个单位,即表示为1,C店在O店的北面2千米处, 可确定点B位于点O右边距离原点2个单位,即表示为2,
(2) 牛奶厂的送货车从O店出发,要把一车牛奶分别送到A,B,C三家经销店, 送货车走的最短路程是从点O到B再到点C再到点A,即2-(-3)+2,然后计算即可求解.
解:(1)能,如图所示:
![]()
(2)依题意得最短路程为2-(-3)+2=7(千米).
答:送货车走的最短路程是7千米.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:
【题目】如图,已知OE是∠AOC的角平分线,OD是∠BOC的角平分线.
(1)若∠AOC=120°,∠BOC=30°,求∠DOE的度数;
(2)若∠AOB=90°,∠BOC=α,求∠DOE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把所有正偶数从小到大排列,并按如下规律分组:
第一组:2,4;
第二组:6,8,10,12;
第三组:14,16,18,20,22,24
第四组:26,28,30,32,34,36,38,40
……
则现有等式Am=(i,j)表示正偶数m是第i组第j个数(从左到右数),如A10=(2,3),则A2018=( )
A. (31,63) B. (32,17) C. (33,16) D. (34,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒![]() cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( )
cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( )

A. ![]() B. 2 C. 2
B. 2 C. 2![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了促进节能减排,倡导节约用电,某市将实行居民生活用电阶梯电价方案,图中折线反映了每户每月用电电费y(元)与用电量x(度)间的函数关系式. 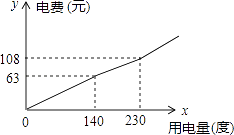
(1)根据图象,阶梯电价方案分为三个档次,填写下表:
档次 | 第一档 | 第二档 | 第三档 |
每月用电量x(度) | 0<x≤140 |
(2)小明家某月用电120度,需交电费元;
(3)求第二档每月电费y(元)与用电量x(度)之间的函数关系式;
(4)在每月用电量超过230度时,每多用1度电要比第二档多付电费m元,小刚家某月用电290度,交电费153元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用简便方法计算:
(1)(-3![]() )+(+8
)+(+8![]() )-(-5
)-(-5![]() );
);
(2)(-![]() )+(+
)+(+![]() )+(+
)+(+![]() )+(-1
)+(-1![]() );
);
(3)(-3![]() )-(-
)-(-![]() )+(-0.5)+3
)+(-0.5)+3![]() ;
;
(4)(+3![]() )+(-2
)+(-2![]() )-(-5
)-(-5![]() )-(+
)-(+![]() );
);
(5)(-0.25)+(-3)-|-1![]() |-(-3);
|-(-3);
(6)(+![]() )+(+17)+(-1
)+(+17)+(-1![]() )-(+7)-(-2
)-(+7)-(-2![]() )+(-
)+(-![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=30°,将△DCB绕点C顺时针旋转60°后,点D的对应点恰好与点A重合,得到△ACE,若AB=3,BC=4,则BD=(提示:可连接BE) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如下图, AB∥CD,点E,F分别为AB,CD上一点.
(1) 在AB,CD之间有一点M(点M不在线段EF上),连接ME,MF,试探究∠AEM,∠EMF,∠MFC之间有怎样的数量关系. 请补全图形,并在图形下面写出相应的数量关系,选其中一个进行证明.

(2)如下图,在AB,CD之间有两点M,N,连接ME,MN,NF,请选择一个图形写出∠AEM,∠EMN,∠MNF,∠NFC 存在的数量关系(不需证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自学:如图1,△ABC中,D是BC边上一点,则△ABD与△ADC有一个相同的高,它们的面积之比等于相应的底之比,记为 ![]() =
= ![]() .
.
(△ABD,△ADC的面积分别用记号S△ABD , S△ADC表示)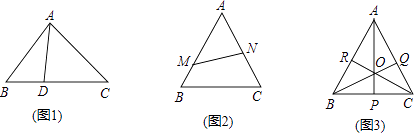
(1)心得:如图1,若BD= ![]() DC,则S△ABD:S△ADC=
DC,则S△ABD:S△ADC=
(2)成长:如图2,△ABC中,M,N分别是AB,AC边上一点,且有AM:MB=2:1,AN:NC=1:1,则△AMN与△ABC的面积比为 .
(3)巅峰:如图3,△ABC中,P,Q,R分别是BC,CA,AB边上的点,且AP,BQ,CR相交于点O,现已知△BPO,△PCO,△COQ,△AOR的面积依次为40,30,35,84,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com