
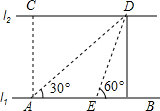
 如图,河的两岸l1与l2互相平行,A、B是l1上的两点,C、D是l2上的两点,某同学在A处测得∠CAB=90°,∠DAB=30°,再沿AB方向走20米到达点E(即AE=20),测得∠DEB=60°.
如图,河的两岸l1与l2互相平行,A、B是l1上的两点,C、D是l2上的两点,某同学在A处测得∠CAB=90°,∠DAB=30°,再沿AB方向走20米到达点E(即AE=20),测得∠DEB=60°.分析 过点D作DF⊥l1于点F.首先证明ED=EF=20,在Rt△DEF中,求出EF即可解决问题.
解答 解:过点D作DF⊥l1于点F.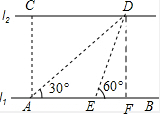
∵l1∥l2,∠CAB=90°,
∴四边形CAFD是矩形,CD=AF,
∵∠DAB=30°,∠DEB=60°,
∴∠ADE=∠DEB-∠DAB=30°,即∠ADE=∠DAE,
∴AE=DE=20,
在Rt△DEF中,∠DFE=90°,∠DEF=60°,DE=20,
∴EF=10,
∴CD=AF=AE+EF=30,
答:C,D两点间的距离是30米.
点评 本题考查勾股定理的应用、解直角三角形、锐角三角函数、等腰三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
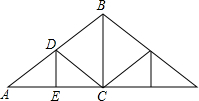 如图,屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=8m,∠A=30°,则BC和DE的长分别等于( )
如图,屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=8m,∠A=30°,则BC和DE的长分别等于( )| A. | 2m,2m | B. | 4m,2m | C. | 2m,4m | D. | 4m,4m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
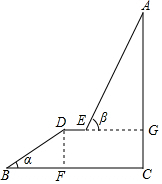 如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车达到A处,返程时从A处乘坐升降电梯直接到达C处;已知:AC⊥BC于C,DE∥BC,BC=110米,DE=10米,BD=60米,BD=60米,α=30°,β=60°,求AC的高度.
如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车达到A处,返程时从A处乘坐升降电梯直接到达C处;已知:AC⊥BC于C,DE∥BC,BC=110米,DE=10米,BD=60米,BD=60米,α=30°,β=60°,求AC的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
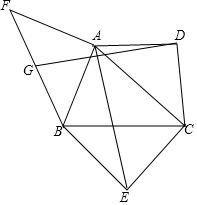 如图所示,已知△ABC是锐角三角形,以边AC、BC为斜边向形外作等腰直角三角形ACD和等腰直角三角形BCE,以边AB为直角边向形外作等腰直角三角形ABF,∠BAF=90°,点G为BF的中点,连接GD和AE,试探究GD和AE的数量关系和位置关系,并对你的结论加以证明.
如图所示,已知△ABC是锐角三角形,以边AC、BC为斜边向形外作等腰直角三角形ACD和等腰直角三角形BCE,以边AB为直角边向形外作等腰直角三角形ABF,∠BAF=90°,点G为BF的中点,连接GD和AE,试探究GD和AE的数量关系和位置关系,并对你的结论加以证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
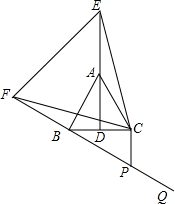 如图,在等边△ABC中,已知AD是∠BAC的角平分线,E为AD延长线上一点,以CE为一边且在CE以左作等边△CEF,连接BF.
如图,在等边△ABC中,已知AD是∠BAC的角平分线,E为AD延长线上一点,以CE为一边且在CE以左作等边△CEF,连接BF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,OA⊥OB,OA=45cm,OB=15cm,一机器人在B处发现有一个小球自A点出发沿着AO方向匀速滚向点O,机器人立即从B处出发以相同的速度匀速直线前进去拦截小球,在点C处截住了小球,求机器人行走的路程BC.
如图所示,OA⊥OB,OA=45cm,OB=15cm,一机器人在B处发现有一个小球自A点出发沿着AO方向匀速滚向点O,机器人立即从B处出发以相同的速度匀速直线前进去拦截小球,在点C处截住了小球,求机器人行走的路程BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com