
 ”表示数据输入、输出框;用“
”表示数据输入、输出框;用“ ”表示数据处理和运算框;用“
”表示数据处理和运算框;用“ ”表示数据判断框(根据条件决定执行两条路径中的某一条)
”表示数据判断框(根据条件决定执行两条路径中的某一条) ”内,应填×5;第二个运算框“
”内,应填×5;第二个运算框“ ”内,应填-3;
”内,应填-3;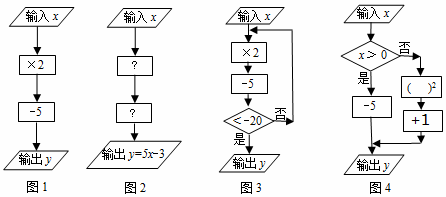
分析 (1)①根据图形列出算式,即可求出答案;
②根据图形列出算式,即可求出答案;
(2)①根据图形列出算式,即可求出答案;
②根据图形列出算式,即可求出答案;
(3)根据图4画出即可.
解答 解:(1)①当x=-2时,y=-2×2-5=-9,
故答案为:-9;
②第一个运算框“×5”内;第二个运算框“-3”内,
故答案为:×5,-3;
(2)①当x=-1时,y=-1×2-5=-7>-20,-7×2-5=-19>-20,-19×2-5=-43<-20,
故答案为:y=-43;
②分为两种情况:当x>0时,x-5=37,
解得:x=42;
当x<0时,x2+1=37,
解得:x=±6,x=6舍去;
故答案为:42或-6;
(3)因为当每月用水量不超过15吨时(含15吨),以2元/吨的价格收费;
当每月用水量超过15吨时,超过部分以3元/吨的价格收费,
所以水费收缴分两种情况,x≤15和x>15,
分别计算,所以可以设计如框图如图.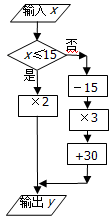 .
.
点评 本题考查了求代数式的值的应用,能读懂图形是解此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,要设计一幅长为60cm,宽为40cm的矩形图案,其中有两横两竖的矩形彩条,横竖彩条宽度比为1:2,若彩条所占面积是图案面积的一半,求一条横彩条的宽度.
如图,要设计一幅长为60cm,宽为40cm的矩形图案,其中有两横两竖的矩形彩条,横竖彩条宽度比为1:2,若彩条所占面积是图案面积的一半,求一条横彩条的宽度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
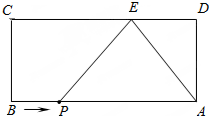 如图,矩形ABCD中,AB=9,AD=4.E为CD边上一点,CE=6.点P从点B出发,以每秒1个单位的速度沿着边BA向终点A运动,连接PE.设点P运动的时间为t秒.
如图,矩形ABCD中,AB=9,AD=4.E为CD边上一点,CE=6.点P从点B出发,以每秒1个单位的速度沿着边BA向终点A运动,连接PE.设点P运动的时间为t秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com