
在平面直角坐标系xOy中,抛物线 交x轴负半轴于点A,交y轴正半轴于点B(0,3),顶点C位于第二象限,连结AB,AC,BC.
交x轴负半轴于点A,交y轴正半轴于点B(0,3),顶点C位于第二象限,连结AB,AC,BC.
(1)求抛物线的解析式;
(2)点D是y轴正半轴上一点,且在B点上方,若∠DCB=∠CAB,请你猜想并证明CD与AC的位置关系;
(3)设与△AOB重合的△EFG从△AOB的位置出发,沿x轴负方向平移t个单位长度(0<t≤3)时,△EFG与△ABC重叠部分的面积为S,求S与t之间的函数关系式.
(1)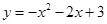 ;(2)
;(2) ;(3)S=
;(3)S=
解析试题分析:(1)先根据抛物线 与y轴交于点B(0,3)求得m的值,再由抛物线的顶点在第二象限,即可得到结果;
与y轴交于点B(0,3)求得m的值,再由抛物线的顶点在第二象限,即可得到结果;
(2)由A(-3,0),B(0,3),C(-1,4)根据勾股定理可求得 ,根据勾股定理的逆定理可得
,根据勾股定理的逆定理可得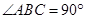 ,再结合∠DCB=∠CAB,即可证得结果;
,再结合∠DCB=∠CAB,即可证得结果;
(3)当0<t≤ 时,如图,EF交AB于点Q,GF交AC于点N,过N做MP//FE交x轴于P点,交BF的延长线点M,BF的延长线交AC于点K,由△AGN∽△KFN根据相似三角形的性质可得
时,如图,EF交AB于点Q,GF交AC于点N,过N做MP//FE交x轴于P点,交BF的延长线点M,BF的延长线交AC于点K,由△AGN∽△KFN根据相似三角形的性质可得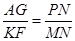 ,即可表示出PN,即可得到结果;当
,即可表示出PN,即可得到结果;当 <t≤3时,如图, EF交AB于点N,交AC于点M,BF交AC于点P,由△AME∽△PMF根据相似三角形的性质可得
<t≤3时,如图, EF交AB于点N,交AC于点M,BF交AC于点P,由△AME∽△PMF根据相似三角形的性质可得 ,即可表示出ME,从而可以求得结果.
,即可表示出ME,从而可以求得结果.
(1) 抛物线
抛物线 与y轴交于点B(0,3)
与y轴交于点B(0,3)
∴
∴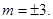
 抛物线的顶点在第二象限,
抛物线的顶点在第二象限,
∴
∴抛物线的解析式为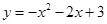 ;
;
(2) A(-3,0),B(0,3),C(-1,4)
A(-3,0),B(0,3),C(-1,4)
∴
∴
∴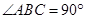
∴
又
∴
∴ ;
;
(3)当0<t≤ 时,如图,EF交AB于点Q,GF交AC于点N,过N做MP//FE交x轴于P点,交BF的延长线点M,BF的延长线交AC于点K
时,如图,EF交AB于点Q,GF交AC于点N,过N做MP//FE交x轴于P点,交BF的延长线点M,BF的延长线交AC于点K
由△AGN∽△KFN
得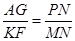
即
解得PN=2t
∴
当 <t≤3时,如图, EF交AB于点N,交AC于点M,BF交AC于点P
<t≤3时,如图, EF交AB于点N,交AC于点M,BF交AC于点P
由△AME∽△PMF
得
即
解得ME=2(3-t)
∴
综上所述:S=
考点:二次函数的综合题
点评:解答本题的关键是读懂题意,画出图形,正确作出辅助线,熟练运用相似三角形的性质及三角形的面积公式解决问题.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
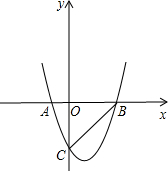 如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.
如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为
如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com