
����Ŀ�� ����������ֱ��������1��2��-3��-4�IJ�����Ƭ�����dz�������֮������ȫ����ͬ�������DZ��泯�ϣ�ϴ�Ⱥ�����ſ�Ƭ������س�ȡһ�Ų��Żأ����ÿ�Ƭ�ϵ����ּ�Ϊm��������س�ȡһ�ţ�����Ƭ�ϵ����ּ�Ϊn��
��1�����û���״ͼ���б���д����m��n�����еĿ��������
��2������ѡ��m��n��ʹһ�κ���y=mx+n��ͼ����һ�����������ĸ��ʣ�
���𰸡���1����1��2����1��-3����1��-4����2��1����2��-3����2��-4����-3��1����-3��2����-3��-4����-4��1����-4��2������-4��-3������2��![]() ��
��
��������
��1���������⻭����״ͼ�����������m��n�����еĿ��������
��2�������ѡ��m��n��ʹһ�κ���y=mx+n��ͼ����һ��������������������ٸ��ݸ��ʹ�ʽ��ʽ���㼴�ɣ�
�⣺��1������״ͼ���£�
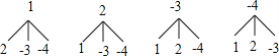
��m��n�����еĿ�������ǣ�1��2����1��-3����1��-4����2��1����2��-3����2��-4����-3��1����-3��2����-3��-4����-4��1����-4��2������-4��-3����
��2����ѡ��m��n��ʹһ�κ���y=mx+n��ͼ����һ����������������У�
��1��-3����1��-4����2��-3����2��-4����4�������
����ʹһ�κ���y=mx+n��ͼ����һ�����������ĸ�����![]() =
=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����н��貿�żƻ��ڳ��й㳡��һ�鳤���οյ�����һ�����Ϊ1500![]() ��ͣ��������ͣ�����������µĿյ�����ͬ������ͨ������֪�����οյصij�Ϊ60
��ͣ��������ͣ�����������µĿյ�����ͬ������ͨ������֪�����οյصij�Ϊ60![]() ����Ϊ40
����Ϊ40![]() ��
��

��1����ͨ���Ŀ��ȣ�
��2��ij��˾ϣ����60��Ԫ�ijа����������㳡�Ĺ��̣��ǽ�������Ϊ���̫����Ҫ���ۣ�ͨ������Э�̣�������48.6��Ԫ���һ�£������ν��۵İٷ�����ͬ����ÿ�ν��۵İٷ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������y1��k1x��ͼ���뷴��������y2��![]() ��x��0����ͼ���ཻ�ڵ�A��
��x��0����ͼ���ཻ�ڵ�A��![]() ��2
��2![]() ������B�Ƿ���������ͼ����һ�㣬���ĺ�������3������OB��AB�����AOB�������_____��
������B�Ƿ���������ͼ����һ�㣬���ĺ�������3������OB��AB�����AOB�������_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
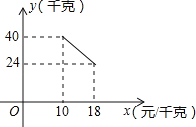
����Ŀ��ij����������һ�ֲ�Ʒ�����ֲ�Ʒ�ijɱ���Ϊ10Ԫ/ǧ�ˣ���֪���ۼ۲����ڳɱ��ۣ�����۲��Ź涨���ֲ�Ʒ�����ۼ۲�����18Ԫ/ǧ�ˣ��г����鷢�֣��ò�Ʒÿ���������y��ǧ�ˣ������ۼ�x��Ԫ/ǧ�ˣ�֮��ĺ�����ϵ��ͼ��ʾ��
��1����y��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2����ÿ�����������W��Ԫ�������ۼ�x��Ԫ/ǧ�ˣ�֮��ĺ�����ϵʽ�������ۼ�Ϊ����ʱ��ÿ����������������������Ƕ��٣�
��3���þ�������Ҫÿ����150Ԫ�������������ۼ�Ӧ��Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪һ�κ���![]() ��ͼ��ֱ���x�ᡢy�ύ�ڵ�A��C���뷴���к���
��ͼ��ֱ���x�ᡢy�ύ�ڵ�A��C���뷴���к���![]() ��ͼ���ڵ�һ�����ڽ��ڵ�P������P��
��ͼ���ڵ�һ�����ڽ��ڵ�P������P��![]() �ᣬ����ΪB����
�ᣬ����ΪB����![]() �����Ϊ9��
�����Ϊ9��

![]() ��A������Ϊ______����C������Ϊ______����P������Ϊ______��
��A������Ϊ______����C������Ϊ______����P������Ϊ______��
![]() ��֪��Q�ڷ���������
��֪��Q�ڷ���������![]() ��ͼ���ϣ��������Ϊ6����x����ȷ��һ��M��ʹ��
��ͼ���ϣ��������Ϊ6����x����ȷ��һ��M��ʹ��![]() ���ܳ���С�������M�����ꣻ
���ܳ���С�������M�����ꣻ
![]() ���E�Ƿ���������
���E�Ƿ���������![]() �ڵ�һ������ͼ���ϵ�һ���㣬�ҵ�E��ֱ��PB���Ҳ࣬����E��
�ڵ�һ������ͼ���ϵ�һ���㣬�ҵ�E��ֱ��PB���Ҳ࣬����E��![]() �ᣬ����ΪF����
�ᣬ����ΪF����![]() ��
��![]() ����ʱ����E�����꣮
����ʱ����E�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y��ax2+bx+cͼ���һ���֣���Գ�����x����1���ҹ��㣨��3��0��������˵������abc��0����2a��b��0����4a+2b+c��0����������5��y1������3��y2���������������㣬��y1��y2������˵����ȷ���ǣ�������
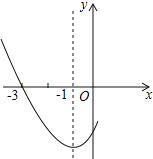
A.�٢�B.�ڢ�C.�٢ڢ�D.�ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ѽ��̳���������ij�ֽ�����Ϊ20Ԫ/������Ʒʱ����30Ԫ/���۳���ÿ�����۳�100�������������������Ʒ���ۼ�ÿ����1Ԫ/�������������ͽ�����2����
��1��Ϊ��ʵ��ÿ��1600Ԫ�����������Ѽ��̳���Ӧ��������Ʒ���ۼ۶�Ϊ���٣�
��2����۾ֹ涨����Ʒ���ۼ۲��ܳ���40Ԫ/�������Ѽ��̳���Ϊ�˻����������Ӧ������Ʒ�ۼ۶�Ϊ���٣���������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����ѧ��ҵ�ؼ��紴ҵ����һ����ֲ�辰�뻨�ܸ�50���ۺ�ͳ�����辰��ƽ��ÿ��������160Ԫ�����ܵ�ƽ��ÿ��������19Ԫ�����з��֣�
���辰ÿ����1�����辰��ƽ��ÿ���������2Ԫ;ÿ����1�����辰��ƽ��ÿ����������2Ԫ;�ڻ��ܵ�ƽ��ÿ������ʼ�ղ���.
С���ƻ��ڶ�����ֲ�辰�뻨�ܹ�100��������ֲ���辰�ȵ�һ������x�����ڶ����辰�뻨������������ֱ�ΪW1��W2����λ��Ԫ��
��1���ú�x�Ĵ���ʽ�ֱ��ʾW1��W2;
��2����xȡ��ֵʱ���ڶ�����ֲ���辰�뻨��������õ�������W���������������Ƕ���?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
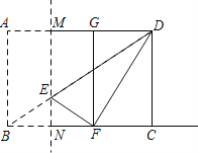
����Ŀ�� ��ͼ���ھ���ABCD�У���NΪ��BC�ϲ���B��C�غϵ�һ�����㣬����N��MN��BC��AD�ڵ�M����BD�ڵ�E����MNΪ�Գ����۵�����ABNM����A��B�Ķ�Ӧ��ֱ���G��F������EF��DF����AB=6��BC=8������DEFΪֱ��������ʱ��CN�ij�Ϊ______��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com