
【题目】已知![]() 是等边三角形,
是等边三角形,![]() .
.
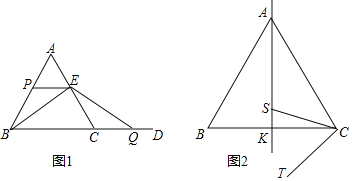
(1)如图1,点![]() 在线段
在线段![]() 上从点
上从点![]() 出发沿射线
出发沿射线![]() 以
以![]() 的速度运动,过点
的速度运动,过点![]() 作
作![]() 交线段
交线段![]() 于点
于点![]() ,同时点
,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 的延长线以
的延长线以![]() 的速度运动,连接
的速度运动,连接![]() 、
、![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
①求证:![]() 是等边三角形;
是等边三角形;
②当点![]() 不与点
不与点![]() 、
、![]() 重合时,求证:
重合时,求证:![]() .
.
(2)如图2,点![]() 为
为![]() 的中点,作直线
的中点,作直线![]() ,点
,点![]() 为直线
为直线![]() 上一点,连接
上一点,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,则点
,则点![]() 在直线
在直线![]() 上运动的过程中,
上运动的过程中,![]() 的最小值是多少?请说明理由.
的最小值是多少?请说明理由.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )
实验次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 2000 |
频率 | 0.365 | 0.328 | 0.330 | 0.334 | 0.336 | 0.332 | 0.333 |
A. 一副去掉大小王的普迺扑克牌洗匀后,从中任抽一张牌的花色是红桃
B. 从一个装有2个白球和1个红球的袋子中任取一球,取到红球的概率
C. 抛一枚硬币,出现正面的概率
D. 抛一个质地均匀的正六面体骰子(六个面上分别标有1,2,3,4,5,6),向上的面点数是5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究:
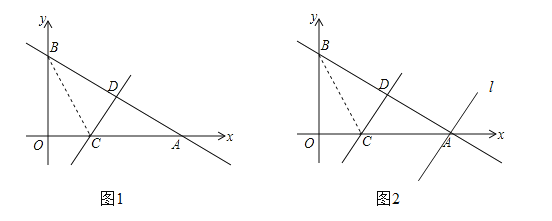
如图1,一次函数![]() 的图象与x轴和y轴分别交于A,B两点,再将△AOB沿直线CD对折,使点A与点B重合.直线CD 与x轴交于点C,与AB交于点D
的图象与x轴和y轴分别交于A,B两点,再将△AOB沿直线CD对折,使点A与点B重合.直线CD 与x轴交于点C,与AB交于点D
(1)求点A和点B的坐标
(2)求线段OC的长度
(3)如图 2,直线 l:y=mx+n,经过点 A,且平行于直线 CD,已知直线 CD 的函数关系式为 ![]() ,求 m,n 的值
,求 m,n 的值
查看答案和解析>>
科目:初中数学 来源: 题型:
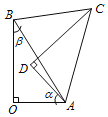
【题目】如图,△AOB≌△ADC,点B和点C是对应顶点,∠O=∠D=90°,记∠OAD=α,∠ABO=β,当BC∥OA时,α与β之间的数量关系为( )
A.α=βB.α=2βC.α+β=90°D.α+β=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
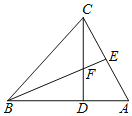
【题目】如图,在△CBD中,CD=BD,CD⊥BD,BE平分∠CBA交CD于点F,CE⊥BE垂足是E,CE的延长线与BD交于点A.
(1)求证:BF=AC;
(2)求证:BE是AC的中垂线;
(3)若BD=2,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在Rt△ABC中,∠ABC=90o,AB是⊙O的直径,⊙O交AC于点D,过点D的直线交BC于点E,交AB的延长线于点P,∠A=∠PDB.
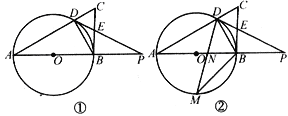
(1)求证:PD是⊙O的切线;
(2)若AB=4,DA=DP,试求弧BD的长;
(3)如图②,点M是弧AB的中点,连结DM,交AB于点N.若tanA=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垫球是排球队常规训练的重要项目之一,下列图表中的数据是运动员甲、乙、丙三人每人10次垫球测试的成绩,测试规则为每次连续接球10个,每垫球到位1个记1分,已知运动员甲测试成绩的中位数和众数都是7.
运动员甲测试成绩统计表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 |
| 6 | 8 | 6 | 8 |
|
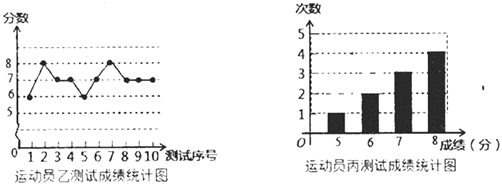
(1)填空:![]() ______;
______;![]() ______.
______.
(2)要从他们三人中选择一位垫球较为稳定的接球能手,你认为选谁更合适?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 某公司的一批某品牌衬衣的质量抽检结果如下:
抽检件数 | 50 | 100 | 200 | 300 | 400 | 500 |
次品件数 | 0 | 4 | 16 | 19 | 24 | 30 |
(1)请结合表格数据直接写出这批衬衣中任抽1件是次品的概率.
(2)如果销售这批衬衣600件,至少要准备多少件正品衬衣供买到次品的顾客退换?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com