
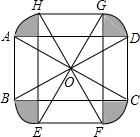
 如图,将矩形ABCD绕对角线的交点0逆时针旋转90°得到矩形EFGH,已知AB=2,BC=2$\sqrt{3}$,则由旋转得到的阴影部分的面积为$\frac{4}{3}$π+4-4$\sqrt{3}$.
如图,将矩形ABCD绕对角线的交点0逆时针旋转90°得到矩形EFGH,已知AB=2,BC=2$\sqrt{3}$,则由旋转得到的阴影部分的面积为$\frac{4}{3}$π+4-4$\sqrt{3}$. 分析 设AD与HF交于K,AD于HE交于M,根据矩形的想知道的AB=2,BC=2$\sqrt{3}$,解直角三角形得到AC=4,∠ADB=30°,根据旋转的性质得到∠DOK=90°,解直角三角形得到OK=tan30°•OD=$\frac{2\sqrt{3}}{3}$,DK=$\frac{4\sqrt{3}}{3}$,AK=$\frac{2\sqrt{3}}{3}$,O到AD的距离=1,根据三角形的面积公式求得S△AOK=$\frac{1}{3}\sqrt{3}$,S△HKM=$\frac{2}{3}$$\sqrt{3}$-1,S扇形AHO=$\frac{1}{3}π$,根据图形面积的和差可得到结论.
解答 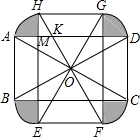 解:设AD与HF交于K,AD于HE交于M,
解:设AD与HF交于K,AD于HE交于M,
在四边形ABCD与四边形EFGH中,
∵AB=2,BC=2$\sqrt{3}$,
∴AC=4,∠ADB=30°,
∴OD=2,
∵将矩形ABCD绕对角线的交点0逆时针旋转90°得到矩形EFGH,
∴∠DOK=90°,
∴OK=tan30°•OD=$\frac{2\sqrt{3}}{3}$,
∴DK=$\frac{4\sqrt{3}}{3}$,
∴AK=$\frac{2\sqrt{3}}{3}$,
∵O到AD的距离=1,
∴S△AOK=$\frac{1}{2}×$$\frac{2}{3}$$\sqrt{3}$×1=$\frac{1}{3}\sqrt{3}$,
∵HM=$\frac{1}{2}$(2$\sqrt{3}$-2)=$\sqrt{3}$-1,
∴MK=tan30°×HM=1-$\frac{\sqrt{3}}{3}$,
∴S△HKM=$\frac{1}{2}$($\sqrt{3}$-1)(1-$\frac{\sqrt{3}}{3}$)=$\frac{2}{3}$$\sqrt{3}$-1,
S扇形AHO=$\frac{30•π×{2}^{2}}{360}$=$\frac{1}{3}π$,
∴阴影部分的面积=4×($\frac{1}{3}π$-$\frac{1}{3}\sqrt{3}$-$\frac{2}{3}$$\sqrt{3}$+1)=$\frac{4}{3}$π+4-4$\sqrt{3}$.
故答案为:$\frac{4}{3}$π+4-4$\sqrt{3}$.
点评 本题考查了旋转的性质,矩形的性质,直角三角形的性质,三角形和扇形面积的计算,正确的识别图形是解题的关键.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:初中数学 来源: 题型:选择题
 如图,将正六边形ABCDEF放置在直角坐标系内,A(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2016次翻转之后,点C的坐标是( )
如图,将正六边形ABCDEF放置在直角坐标系内,A(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2016次翻转之后,点C的坐标是( )| A. | (4032,0) | B. | (4032,2$\sqrt{3}$) | C. | (4031,$\sqrt{3}$) | D. | (4033,$\sqrt{3}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
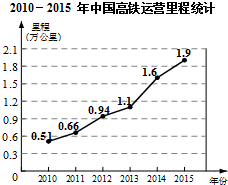 我国2010-2015年高铁运营里程情况统计如图所示,根据统计图提供的信息,预估2016年我国高铁运营里程约为2.2万公里,你的预估理由是每年平均增长量近似相等.
我国2010-2015年高铁运营里程情况统计如图所示,根据统计图提供的信息,预估2016年我国高铁运营里程约为2.2万公里,你的预估理由是每年平均增长量近似相等.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>-$\frac{5}{2}$ | B. | m≥-2 | C. | m<-1 | D. | m≤-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在空白网格内将某一个小正方形涂成阴影部分,且所涂的小正方形与原阴影图形的小正方形至少有一边重合.小红按要求涂了一个正方形,所得到的阴影图形恰好是轴对称图形的概率为( )
如图,在空白网格内将某一个小正方形涂成阴影部分,且所涂的小正方形与原阴影图形的小正方形至少有一边重合.小红按要求涂了一个正方形,所得到的阴影图形恰好是轴对称图形的概率为( )| A. | $\frac{1}{5}$ | B. | $\frac{4}{15}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
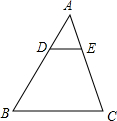 如图,在△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,则下列结论中正确的是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,则下列结论中正确的是( )| A. | $\frac{AE}{AC}$=$\frac{1}{2}$ | B. | $\frac{DE}{BC}$=$\frac{1}{2}$ | ||
| C. | $\frac{△ADE的周长}{△ABC的周长}$=$\frac{1}{3}$ | D. | $\frac{△ADE的面积}{△ABC的面积}$=$\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com