练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．如图，已知AB=BC，AD=CD，求证：AE=CE．

    分析 首先证明△ABD≌△BCD得到∠1=∠2，再证明△ADE≌△CDE即可．

    解答 解：在△ABD和△BCD中，
    ∵$\left\{\begin{array}{l}{AB=BC}\\{AD=CD}\\{BD=BD}\end{array}\right.$，
    ∴△ABD≌△BCD，
    ∴∠1=∠2，
    在△ADE和△CDE中，
    ∵$\left\{\begin{array}{l}{AD=CD}\\{∠1=∠2}\\{DE=DE}\end{array}\right.$，
    ∴△ADE≌△CDE，
    ∴AE=CE．

    点评 本题主要考查了全等三角形的判定与性质，解题的关键是证明△ABD≌△BCD得到∠1=∠2，此题难度不大．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    15．一克黄金260元，买x克黄金的总价为y元，则y与x的关系式为y=260x．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图，A，F，E，B四点在同一直线上，AC⊥CE，BD⊥DF，AF=BE，AC=BD．试判断DF与CE的关系（指数量与位置关系），并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．某中学为调查本校学生周末平均每天做作业所用时间的情况，随机调查了50名同学，如图是根据调查所得数据绘制的统计图的一部分．请根据以上信息，解答下列问题：

    （1）在这次调查的数据中，做作业所用时间的众数是3，中位数是3，平均数是3，并补全统计图；
    （2）若该校共有1500名学生，根据以上调查结果估计该校全体学生每天做作业时间在3小时内（含3小时）的同学共有多少人．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．已知三角形的三边长分别为3，x-2，5，求x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．计算：
    （1）$\frac{3x}{x-4y}$+$\frac{x+y}{4y-x}$-$\frac{7y}{x-4y}$；
    （2）（-2）-3+（-$\frac{1}{2}$）-4+2-1×2-3-（π-3.14）0；
    （3）$\frac{{x}^{2}}{x-1}$-x-1；
    （4）（$\frac{x}{x-y}$-$\frac{2y}{x-y}$）•$\frac{xy}{x-2y}$×（$\frac{1}{x}$-$\frac{1}{y}$）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．如图所示，有一个圆柱，它的高为9厘米，底面周长为24厘米，在圆柱下底面的A点有一只蚂蚁要沿侧面到上底面B点取食物，问它爬行的最短路程是多少厘米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．先化简，再求值：（3a-b）2-b2-9a（a-b），其中a=$\frac{7}{9}$，b=$\frac{3}{14}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

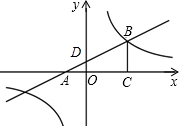    15．如图，平面直角坐标系中，直线y=$\frac{1}{2}$x+$\frac{1}{2}$与x轴交于点A，与y轴交于点D，与双曲线y=$\frac{k}{x}$在第一象限内交于点B，BC⊥x轴于点C，AB=3AD．求双曲线的解析式．

    查看答案和解析>>

    同步练习册答案