
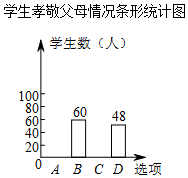
 某校为了了解学生孝敬父母的情况(选项:A.为父母洗一次脚;B.帮父母做一次家务;C.给父母买一件礼物;D.其它),在全校范围内随机抽取了若干名学生进行调查,得到如图表(部分信息未给出):根据以上信息解答下列问题:
某校为了了解学生孝敬父母的情况(选项:A.为父母洗一次脚;B.帮父母做一次家务;C.给父母买一件礼物;D.其它),在全校范围内随机抽取了若干名学生进行调查,得到如图表(部分信息未给出):根据以上信息解答下列问题:| 选项 | 频数 | 频率 |
| A | m | 0.15 |
| B | 60 | p |
| C | n | 0.4 |
| D | 48 | 0.2 |
分析 (1)根据题意可以求得本次调查的学生数,从而可以求得m、n、p的值;
(2)根据统计图中的数据可以求得本次调查的学生数并把统计图补充完整;
(3)根据统计图表格中的数据可以估计该校全体学生中选择B选项的有多少人.
解答 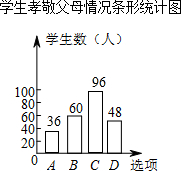 解:(1)由统计图可得,
解:(1)由统计图可得,
本次抽查的学生有:48÷0.2=240(人),
m=240×0.15=36,n=240×0.4=96,p=60÷240=0.25,
故答案为:36,96,0.25;
(2)由统计图可得,
本次抽查的学生有:48÷0.2=240(人),
由(1)知,m=36,n=96,补全的条形统计图如右图所示;
(3)由题意可得,
该校全体学生中选择B选项的有:1600×0.25=400(人),
即该校全体学生中选择B选项的有400人.
点评 本题考查条形统计图、用样本估计总体、频数分布表,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
| 摸球次数 | 40 | 80 | 120 | 160 | 200 | 240 | 280 | 320 | 360 | 400 |
| 出现红色的频数 | 14 | 24 | 38 | 68 | 77 | 92 | 109 | 120 | 132 | |
| 出球红色的频率 | 35% | 32% | 35% | 34% | 33% | 34% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
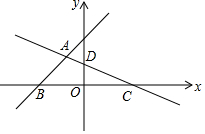 如图,在平面直角坐标系中,直线y=x+3与x轴交于点B,与直线CD交于点A(-$\frac{12}{11}$,a),点D的坐标为(0,$\frac{3}{2}$),点C在x轴上
如图,在平面直角坐标系中,直线y=x+3与x轴交于点B,与直线CD交于点A(-$\frac{12}{11}$,a),点D的坐标为(0,$\frac{3}{2}$),点C在x轴上查看答案和解析>>
科目:初中数学 来源: 题型:解答题
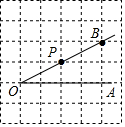 点P是∠AOB的边OB上一点.
点P是∠AOB的边OB上一点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
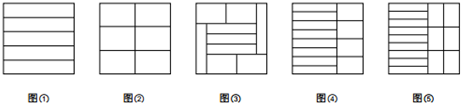
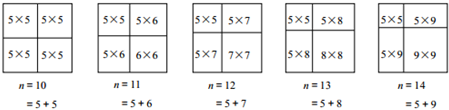
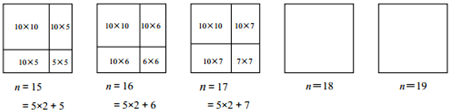
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com