
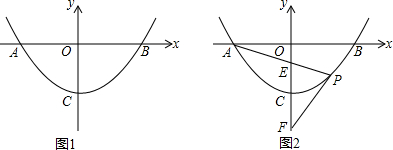
分析 (1)①根据待定系数法求函数解析式,可得答案;
②根据平行线的判定,可得PD∥OB,根据函数值相等两点关于对称轴对称,可得D点坐标;
(2)作PQ⊥AB于Q点,设P(m,am2+c),A(-t,0),B(t,0),可表示出OE、OF的长,可得答案.
解答 解:
(1)①将P(1,-3),B(4,0)代入y=ax2+c,得$\left\{\begin{array}{l}{16a+c=0}\\{a+c=-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\frac{1}{5}}\\{c=-\frac{16}{5}}\end{array}\right.$,
∴抛物线的解析式为y=$\frac{1}{5}$x2-$\frac{16}{5}$;
②如图1,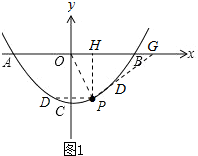
当点D在OP左侧时,
由∠DPO=∠POB,得DP∥OB,
∴D与P关于y轴对称,且P(1,-3),
∴D(-1,-3);
当点D在OP右侧时,延长PD交x轴于点G.
作PH⊥OB于点H,则OH=1,PH=3.
∵∠DPO=∠POB,
∴PG=OG.
设OG=x,则PG=x,HG=x-1.
在Rt△PGH中,由x2=(x-1)2+32,得x=5.
∴点G(5,0).
∴直线PG的解析式为y=$\frac{3}{4}$x-$\frac{15}{4}$,
解方程组$\left\{\begin{array}{l}{y=\frac{3}{4}x-\frac{15}{4}}\\{y=\frac{1}{5}{x}^{2}-\frac{16}{5}}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=-3}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{11}{4}}\\{y=-\frac{27}{16}}\end{array}\right.$,.
∵P(1,-3),
∴D($\frac{11}{4}$,-$\frac{27}{16}$).
∴点D的坐标为(-1,-3)或($\frac{11}{4}$,-$\frac{27}{16}$).
(2)点P运动时,OE+OF是定值,理由如下:
如图2,作PQ⊥AB于Q点,
设P(m,am2+c),A(-t,0),B(t,0),则at2+c=0,c=-at2.
∵PQ∥OF,
∴$\frac{PQ}{OF}$=$\frac{BQ}{BO}$,
∴OF=$\frac{PQ•BO}{BQ}$=-$\frac{-(a{m}^{2}+c)t}{t-m}$=$\frac{(a{m}^{2}-a{t}^{2})t}{m-t}$═amt+at2.
同理OE=-amt+at2,
∴OE+OF=2at2=-2c=2OC=$\frac{16}{5}$.
点评 本题为二次函数综合应用,涉及待定系数法、平行线的判定和性质、函数图象的交点、方程思想等知识.在(1)①中注意利用待定系数法求函数解析式,在②利用函数值相等的点关于对称轴对称得出D点坐标是解题关键;在(2)用平行线分线段成比例表示出OE、OF的长是解题关键.本题考查知识点较多,综合性较强,难度适中.


科目:初中数学 来源: 题型:选择题
| A. | 掷一枚硬币,着地时反面向上 | |
| B. | 买一张福利彩票中奖了 | |
| C. | 投掷3枚骰子,面朝上的三个数字之和为18 | |
| D. | 五边形的内角和为540度 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
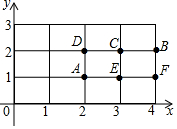 如图,若用A(2,1)表示放置2个胡萝卜,1棵小白菜;点B(4,2)表示放置4个胡萝卜,2棵小白菜:
如图,若用A(2,1)表示放置2个胡萝卜,1棵小白菜;点B(4,2)表示放置4个胡萝卜,2棵小白菜:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
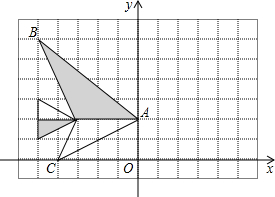 如图,下列网格中,每个小正方形的边长都是1,图中“小鱼”的各个顶点都在格点上.
如图,下列网格中,每个小正方形的边长都是1,图中“小鱼”的各个顶点都在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
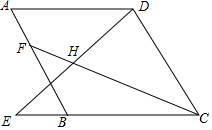 如图,在?ABCD中,AD=CD,AB=14.点E在CB的延长线上,点F在AB边上,连接DE、CF相交于点H,若∠CHD=∠A.BF=11,CF=20,则线段BE的长为$\frac{35}{11}$.
如图,在?ABCD中,AD=CD,AB=14.点E在CB的延长线上,点F在AB边上,连接DE、CF相交于点H,若∠CHD=∠A.BF=11,CF=20,则线段BE的长为$\frac{35}{11}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a-3<b-3 | B. | $\frac{a}{3}$>$\frac{b}{3}$ | C. | 3a>2b | D. | 3+a>3+b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com