Question

已知等腰三角形的周长为16，底边为y，腰长为x，
（1）求y与x的函数关系式；
（2）求出自变量x的取值范围；
（3）画出该函数的图象．

Answer 1

解：（1）由题意得，2x+y=16，
则y=16-2x；

（2）根据三角形的三边关系得x-x＜y＜x+x，即0＜y＜2x，
又∵y=16-2x，
∴0＜16-2x＜2x，
解得：4＜x＜8，
故可得自变量x的取值范围为4＜x＜8．

（3）y=16-2x（4＜x＜8）的图象如下：

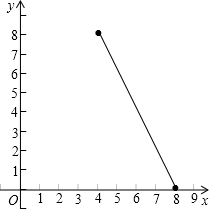
分析：（1）根据三角形的面积公式即可确定y与x的函数关系式；
（2）由三角形的三边关系，可得出自变量x的取值范围；
（3）利用两点法作出函数图象即可．
点评：本题考查了一次函数的应用及三角形的三边关系：两边之和大于第三边，两边之差小于第三边．