
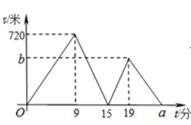
【题目】甲、乙二人从学校出发去科技馆,甲步行一段时间后,乙骑自行车沿相同路线行进,两人均匀速前行,他们的路程差S(米)与甲出发时间t(分)之间的函数关系如图所示.下列说法:①乙先到达科技馆;②乙的速度是甲速度的2.5倍;③b=480;④a=24.其中,正确的是 ______(填序号).
【答案】①②③.
【解析】
根据甲步行720米,需要9分钟,进而得出甲的运动速度,利用图形得出乙的运动时间以及运动距离,进而分别判断得出答案.
由图象得出甲步行720米,需要9分钟,
所以甲的运动速度为:720÷9=80(m/分),
当第15分钟时,乙运动159=6(分钟),
运动距离为:15×80=1200(m),
∴乙的运动速度为:1200÷6=200(m/分),
∴200÷80=2.5,(故②正确);
当第19分钟以后两人之间距离越来越近,说明乙已经到达终点,则乙先到达科技馆,(故①正确);
此时乙运动199=10(分钟),
运动总距离为:10×200=2000(m),
∴甲运动时间为:2000÷80=25(分钟),
故a的值为25,(故④错误);
∵甲19分钟运动距离为:19×80=1520(m),
∴b=20001520=480,(故③正确).
故答案为:①②③.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,下列4个三角形中,均有AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是( )

A. ①③B. ①②④C. ①③④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某巡逻车在一条南北大道上巡逻,某天巡逻车从岗亭A处出发,规定向北方向为正,向南方向为负,当天行驶记录如下(单位:千米) ![]() .
.
(1)最终巡逻车是否回到岗亭![]() 处?若没有,请描述巡逻车的位置:
处?若没有,请描述巡逻车的位置:
(2)若巡逻车行驶1千米耗油0.1升,出发时油箱有油5升,请问途中需要加油吗?若需要,途中至少还需补充多少升油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.

(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h(甲车休息前后的速度相同),甲、乙两车行驶的路程y(km)与行驶的时间x(h)的函数图象如图所示.根据图象的信息有如下四个说法:
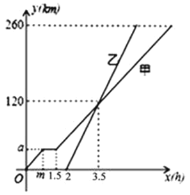
①甲车行驶40千米开始休息
②乙车行驶3.5小时与甲车相遇
③甲车比乙车晚2.5小时到到B地
④两车相距50km时乙车行驶了![]() 小时
小时
其中正确的说法有( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
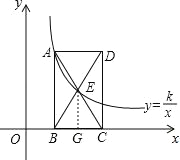
【题目】已知如图:点(1,3)在函数y=![]() (x>0)的图象上,矩形ABCD的边BC在x轴上,E是对角线BD的中点,函数y=
(x>0)的图象上,矩形ABCD的边BC在x轴上,E是对角线BD的中点,函数y=![]() (x>0)的图象又经过A、E两点,点E的横坐标为m,解答下列问题:
(x>0)的图象又经过A、E两点,点E的横坐标为m,解答下列问题:
(1)求k的值;
(2)求点A的坐标;(用含m代数式表示)
(3)当∠ABD=45°时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面四个生产生活现象,可以用“两点之间,线段最短”来解释的是( )
A.用两颗钉子就可以把木条固定在墙上
B.从![]() 地到
地到![]() 地架设电线沿线段
地架设电线沿线段![]() 来架设
来架设
C.植树时定出两棵树的位置后确定同一行树所在的直线
D.打靶的时候,眼睛要与枪上的准星、靶心在同一条直线上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() .
.
(1)![]() 满足何条件时,y随x的增大而减小;
满足何条件时,y随x的增大而减小;
(2)![]() 满足何条件时,图像经过第一、二、四象限;
满足何条件时,图像经过第一、二、四象限;
(3)![]() 满足何条件时,它的图像与y轴的交点在x轴的上方.
满足何条件时,它的图像与y轴的交点在x轴的上方.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,解决后面两个问题:
一个能被17整除的自然数我们称为“灵动数”.“灵动数”的特征是:若把一个整数的个位数字截去,再从余下的数中,减去个位数的5倍,如果差是17的整倍数(包括0),则原数能被17整除.如果差太大或心算不易看出是否是17的倍数,就继续上述的“截尾、倍大、相减、验差”的过程,直到能清楚判断为止.
例如:判断1675282能不能被17整除. 167528﹣2×5=167518,16751﹣8×5=16711,1671﹣1×5=1666,166﹣6×5=136,到这里如果你仍然观察不出来,就继续…6×5=30,现在个位×5=30>剩下的13,就用大数减去小数,30﹣13=17,17÷17=1;所以1675282能被17整除.
(1)请用上述方法判断7242和2098754 是否是“灵动数”,并说明理由;
(2)已知一个四位整数可表示为![]() ,其中个位上的数字为n,十位上的数字为m,0≤m≤9,0≤n≤9且m,n为整数.若这个数能被51整除,请求出这个数.
,其中个位上的数字为n,十位上的数字为m,0≤m≤9,0≤n≤9且m,n为整数.若这个数能被51整除,请求出这个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com