
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]()
(Ⅰ)求证:方程有两个不相等的实数根;
(Ⅱ)若此方程的一个根是1,请求出方程的另一个根;
(Ⅲ)求以(Ⅱ)中所得两根为边长的等腰三角形的周长.
【答案】(Ⅰ) 见解析;(Ⅱ) 3;(Ⅲ)7.
【解析】
(Ⅰ)根据关于x的方程x2-(m+2)x+(2m-1)=0的根的判别式的符号来证明结论;
(Ⅱ)根据一元二次方程的解的定义求得m值,然后由根与系数的关系求得方程的另一根,分两种情况进行讨论解答即可;
(Ⅲ)根据三角形三边的关系讨论即可.
(Ⅰ)证明:∵△=(m+2)2-4(2m-1)=(m-2)2+4,
∴在实数范围内,m无论取何值,(m-2)2+4≥4,
即△≥4,
∴关于x的方程x2-(m+2)x+(2m-1)=0恒有两个不相等的实数根;
(Ⅱ)根据题意,得12-1×(m+2)+(2m-1)=0,
解得,m=2,
则方程的另一根为:m+2-1=2+1=3;
(Ⅲ)①当该等腰三角形的腰为1、底边为3时,
∵1+1<3,
∴构不成三角形;
②当该等腰三角形的腰为3、底边为1时,等腰三角形的周长=3+3+1=7.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD. 
(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,已知直线l1经过原点O 及A(2,2 ![]() )两点,将直线l1向右平移4个单位后得到直线l2 , 直线l2与x 轴交于点B.
)两点,将直线l1向右平移4个单位后得到直线l2 , 直线l2与x 轴交于点B. 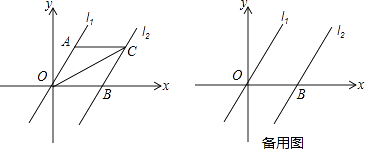
(1)求直线l2的函数表达式;
(2)作∠AOB 的平分线交直线l2于点C,连接AC.求证:四边形OACB是菱形;
(3)设点P 是直线l2上一点,以P 为圆心,PB 为半径作⊙P,当⊙P 与直线l1相切时,请求出圆心P 点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的边BC在直线l上,AC⊥BC,且AC=BC,△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP.
(1)在图①中,请你通过观察、测量、猜想,写出AB与AP所满足的数量关系和位置关系;
(2)将△EFP沿直线l向左平移到图②的位置时,EP交AC于点Q,连接AP,BQ,猜想并写出BQ与AP所满足的数量关系和位置关系,请证明你的猜想;
(3)将△EFP沿直线l向左平移到图③的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ,你认为(2)中所猜想的BQ与AP的数量关系与位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AC=3,BC=4,点P为AB边上任一点,过P分别作PE⊥AC于E,PF⊥BC于F,则线段EF的最小值是__________.
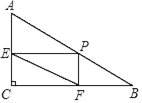
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售甲、乙两种品牌的智能手机.这两种手机的进价和售价如下表所示:
甲 | 乙 | |
进价(元/部) | 4400 | 2000 |
售价(元/部) | 5000 | 2500 |
该商场计划购进两种手机若干部,共需14.8万元,预计全部销售后可获毛利润共2.7万元.(毛利润=(售价一进价)×销售量)
(Ⅰ)该商场计划购进甲、乙两种手机各多少部?
(II)通过市场调研,该商场决定在原计划的基础上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的3倍,而且用于购进这两种手机的总资金不超过156万元,该商场应该怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,角平分线AD、BE、CF相交于点H,过H点作HG⊥AC,垂足为G,那么∠AHE和∠CHG的大小关系为( )
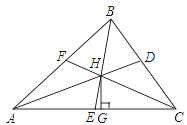
A. ∠AHE>∠CHG B. ∠AHE<∠CHG C. ∠AHE=∠CHG D. 不一定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解家长关注孩子成长方面的状况,学校开展了针对学生家长的“您最关心孩子哪方面成长”的主题调查,调查设置了“健康安全”、“日常学习”、“习惯养成”、“情感品质”四个项目,并随机抽取甲、乙两班共100位学生家长进行调查,根据调查结果,绘制了如图不完整的条形统计图. 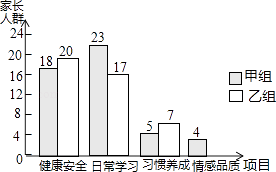
(1)补全条形统计图.
(2)若全校共有3600位学生家长,据此估计,有多少位家长最关心孩子“情感品质”方面的成长?
(3)综合以上主题调查结果,结合自身现状,你更希望得到以上四个项目中哪方面的关注和指导?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有客房50间,当每间客房每天的定价为220元时,客房会全部住满;当每间客房每天的定价增加10元时,就会有一间客房空闲,设每间客房每天的定价增加x元时,客房入住数为y间.
(1)求y与x的函数关系式(不要求写出x的取值范围);
(2)如果每间客房入住后每天的各种支出为40元,不考虑其他因素,则该宾馆每间客房每天的定价为多少时利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com