

���� ��1���������ε����ʵõ���AOG�ա�DOG���ɣ�
��2���ɡ�AOG�ա�DOG�õ����ۣ��ٽ��ͬ�ǻ�Ƚǵ������������EOF��
��3���жϳ�OF��ֱƽ��EG�������ܳ����ɣ�
��4�����жϳ���AOF�ס�CEO���ó�$\frac{{S}_{��AOF}}{{S}_{��CEO}}=\frac{AF}{CE}$�����$\frac{OF}{OE}$��
��� �⣺��1��OE=OG��
���ɣ���ͼ1��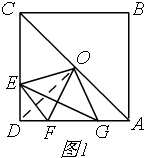
����OD����������ABCD��
�ߵ�O�����������ģ�
��OA=OD����OAD=��ODC=45�㣬
��AG=DE��
���AOG�ա�DOG��
��OE=OG��
��2����EOF�Ķ������ᷢ���仯��
���ɣ��ɣ�1����֪����AOG�ա�DOE��
���DOE=��AOG��
�ߡ�AOG+��DOG=90�㣬
���DOE+��DOG=90�㣬
���DOE=��AOG��
�ߡ�EOG=90�㣬
��OE=OG��OF��EG��
���EOF=45�㣬
���Ϊ��ֵ��
��3���ɣ�2����֪��OE=OG��OF��EG��
��OF��ֱƽ��EG��
���DEF���ܳ�ΪDE+EF+DF=AG+FG+DF=AD��
��a=6��
���DEF���ܳ�ΪAD=a=6����0��DE��3��
��4������ͼ2��
�ߡ�EOF=45�㣬
���COE+AOF=135��
�ߡ�OAF=45�㣬
���AFO+��AOF=135�㣬
���COE=��AFO��
���AOF�ס�CEO��
��$\frac{{S}_{��AOF}}{{S}_{��CEO}}=��\frac{0F}{OE}��^{2}$��
��O��AF��CE�ľ�����ȣ�
��$\frac{{S}_{��AOF}}{{S}_{��CEO}}=\frac{AF}{CE}$��
�ࣨ$\frac{OF}{OE}$��2=$\frac{AF}{CE}=\frac{36}{25}$��
��$\frac{OF}{OE}$��0��
��$\frac{OF}{OE}$=$\frac{6}{5}$��
�ڲ��룺S=$\frac{1}{2}$a2��
���ɣ���ͼ3��
�ɣ�1����֪����AOF�ס�CEO��
��$\frac{AF}{OC}=\frac{OA}{CE}$��
��AF��CE=OA��OC��
��EH��AB��FG��CB����B=90�㣬
��S=AF��CE��
��S=OA��OC=$\frac{\sqrt{2}a}{2}$��$\frac{\sqrt{2}a}{2}$=$\frac{1}{2}$a2��
���� �������ı����ۺ��⣬��Ҫ���������ε����ʣ��߶εĴ�ֱƽ���ߵ��ж������ʣ����������ε����ʺ��ж����Ȿ��Ĺؼ��ǽǶȵļ��㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
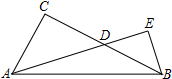 ��ͼ���ڡ�ABC�У���C=90�㣬��D��BC����һ���㣬����B��BE��AD��AD���ӳ�����E����AC=6��BC=8����$\frac{DE}{AD}$�����ֵΪ��������
��ͼ���ڡ�ABC�У���C=90�㣬��D��BC����һ���㣬����B��BE��AD��AD���ӳ�����E����AC=6��BC=8����$\frac{DE}{AD}$�����ֵΪ��������| A�� | $\frac{1}{2}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{3}{4}$ | D�� | $\frac{\sqrt{2}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ������ȤС��20λͬѧ��ʵ������еĵ÷���������
������ȤС��20λͬѧ��ʵ������еĵ÷���������| �÷֣��֣� | 10 | 9 | 8 | 7 |
| �������ˣ� | 5 | 8 | 4 | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����O�ǡ�ABC�����Բ��AB��ֱ������D��$\widehat{AC}$���е㣬EΪBA�ӳ�����һ�㣬�ҡ�DEB=��CDB
��ͼ����O�ǡ�ABC�����Բ��AB��ֱ������D��$\widehat{AC}$���е㣬EΪBA�ӳ�����һ�㣬�ҡ�DEB=��CDB�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com