
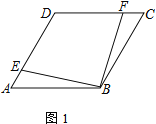
【题目】四边形ABCD为菱形,点E在边AD上,点F在边CD上
(1) 若AE=CF,求证:EB=BF
(2) 若AD=4,DE=CF,且△EFB为等边三角形,求四边形DEBF的面积
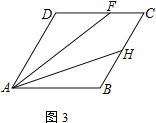
(3) 若∠DAB=60°,点H在边BC上,且BH=HC=2.若∠DFA=2∠HAB,直接写出CF的长
【答案】(1)见解析;(2)S四边形DEBF=![]() ;(3)
;(3)![]() ;
;
【解析】
(1)因为四边形ABCD为菱形,得出AB=BC,∠EAB=∠FBC,又由AE=CF,得出△ABE≌△BCF(SAS),进而得出EB=BF.
(2)连接BD,截取AH=CF,由(1)中得知,△ABE≌△BCF(SAS),得出BH=BF=BE,进而可知∠BHE=∠BEH,∠AHB=∠BED,从而可判定△DEB≌△AHB,得出AB=BD,可判定△DEB≌△CFB,进而得出四边形DEBF的面积等于菱形ABCD面积减去三角形ABD面积,即为三角形ABD的面积,即可得解.
(3)延长AD,作FM⊥AM,交于M,延长DC、AH交于点K,由∠DFA=2∠HAB=∠FAK+∠HAB,可得出∠FAK=∠HAB=∠FKA,进而得出AF=FK,因此DF=4-CF,DM=2-![]() CF,MF=
CF,MF=![]() (4-CF),进而得出AM=4+2-
(4-CF),进而得出AM=4+2-![]() CF=6-
CF=6-![]() CF,根据勾股定理,
CF,根据勾股定理,![]()
进而得出关于CF的方程,即可求出CF.
(1) 证明:∵四边形ABCD为菱形,
∴AB=BC,∠EAB=∠FBC,
又∵AE=CF,
∴△ABE≌△BCF(SAS)
∴EB=BF.
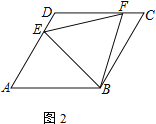
(2)如图所示,连接BD,截取AH=CF
由(1)中得知,△ABE≌△BCF(SAS)
∴BH=BF=BE
∴∠BHE=∠BEH
∴∠AHB=∠BED
∴△DEB≌△AHB,
∴AB=BD
∴△DEB≌△CFB,
∴四边形DEBF的面积等于菱形ABCD面积减去三角形ABD面积,即为三角形ABD的面积,
S四边形DEBF=![]() =
=![]()
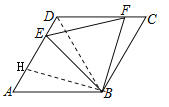
(3)如图所示,延长AD,作FM⊥AM,交于M,延长DC、AH交于点K,
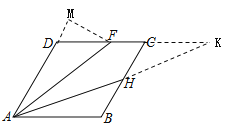
∵∠DFA=2∠HAB=∠FAK+∠HAB
∴∠FAK=∠HAB=∠FKA
∴AF=FK
∴DF=4-CF,DM=2-![]() CF,MF=
CF,MF=![]() (4-CF),
(4-CF),
∴AM=4+2-![]() CF=6-
CF=6-![]() CF
CF
又![]()
![]()
∴CF=![]()


科目:初中数学 来源: 题型:
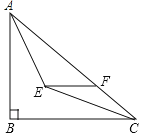
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,∠BAC,∠ACB的平分线相交于点E,过点E作EF∥BC交AC于点F,则EF的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
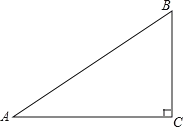
【题目】如图,在△ABC中,∠C=90°,AC=8,BC=6,点D是AB的中点,点E在边AC上,将△ADE沿DE翻折,使点A落在点A′处,当A′E⊥AC时,A′B=_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
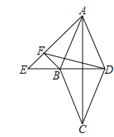
【题目】如图,点E在菱形ABCD的对角线DB的延长线上,且∠AED=45°,过B作AE的垂线交AE于F,连接FD.当∠AFD=60°时,![]() =___________
=___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某条公共汽车线路收支差额![]() 与乘客量
与乘客量![]() 的函数关系如图所示(收支差额
的函数关系如图所示(收支差额![]() 车票收入
车票收入![]() 支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变支出费用,提高车票价格;建议(Ⅱ)不改变车票价格,减少支出费用. 下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )
支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变支出费用,提高车票价格;建议(Ⅱ)不改变车票价格,减少支出费用. 下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )
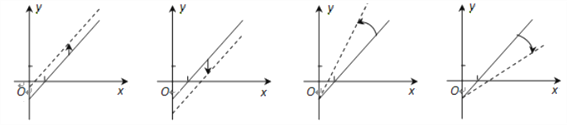
④ ③ ② ①
A. ①反映了建议(Ⅰ),③反映了建议(Ⅱ) B. ②反映了建议(Ⅰ),④反映了建议(Ⅱ)
C. ①反映了建议(Ⅱ),③反映了建议(Ⅰ) D. ②反映了建议(Ⅱ),④反映了建议(Ⅰ)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解全校学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.同时把调查得到的结果绘制成如图所示的条形统计图和扇形统计图(均不完整).请根据图中提供的信息解答下列问题:
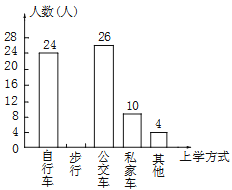
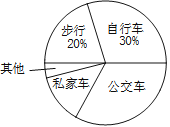
(1)在这次调查中,一共抽取了多少名学生?
(2)通过计算补全条形统计图;
(3)在扇形统计图中,“公交车”部分所对应的圆心角是多少度?
(4)若全校有1600名学生,估计该校乘坐私家车上学的学生约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
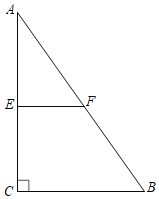
【题目】如图,在直角三角形ABC中,∠C=90°,∠B=60°,AB=8cm,E、F分别为边AC、AB的中点.
(1)求∠A的度数;
(2)求EF和AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
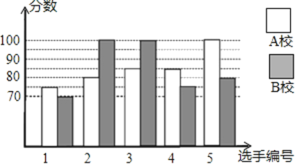
(1)根据图示填写下表:

(2)结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
(3)计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式(组):
(Ⅰ)解不等式:![]() <
<![]()
(Ⅱ)解不等式组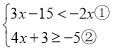
请结合题意填空,完成本题的解答;
(1)解不等式①,得: ;
(2)解不等式②,得: ;
(3)把不等式①和②的解集在如图数轴上表示出来;
![]()
(4)原不等式组的解集为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com