
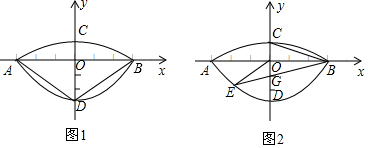
 如图,AB为⊙O的直径,弦BC,DE相交于点F,且DE⊥AB于点G,过点C作⊙O的切线交DE的延长线于点H.
如图,AB为⊙O的直径,弦BC,DE相交于点F,且DE⊥AB于点G,过点C作⊙O的切线交DE的延长线于点H.分析 (1)连接OC,想办法想办法证明∠2=∠5即可.
(2)思路一:①OF过圆心且点F是BC的中点,由垂径定理可得BC=2CF,∠OFC=90°;②由∠6与∠1互余,∠2与∠1互余可得∠6=∠2,从而可知tan∠6=m;③在Rt△OFC中,由$tan∠6=\frac{CF}{OF}=m$,可设OF=x,CF=mx,由勾股定理,得x2+(mx)2=52,可解得x的值;④由BC=2CF=2mx,可求BC的长.
思路二:①由AB是⊙O的直径,可得△ACB是直角三角形,知∠6与∠4互余,又DE⊥AB可知∠3与∠4互余,得∠6=∠3;②由∠6=∠3,∠3=∠2,可得∠6=∠2,从而可知tan∠6=m;③在Rt△ACB中,由$tan∠6=\frac{BC}{AC}=m$,可设AC=x,BC=mx,由勾股定理,得x2+(mx)2=102,可解得x的值;④由BC=mx,可求BC的长.
解答 (1)证明:连接OC,如图1.
∵CH是⊙O的切线,
∴∠2+∠1=90°,
∵DE⊥AB,
∴∠3+∠4=90°,
∵OB=OC,
∴∠1=∠4,
∴∠2=∠3,
又∵∠5=∠3,
∴∠2=∠5,
∴HC=HF.
(2)求解思路如下:
思路一:连接OF,如图2.
①OF过圆心且点F是BC的中点,由垂径定理可得BC=2CF,∠OFC=90°;
②由∠6与∠1互余,∠2与∠1互余可得∠6=∠2,从而可知tan∠6=m;
③在Rt△OFC中,由$tan∠6=\frac{CF}{OF}=m$,可设OF=x,CF=mx,由勾股定
理,得x2+(mx)2=52,可解得x的值;
④由BC=2CF=2mx,可求BC的长.
思路二:连接AC,如图3.
①由AB是⊙O的直径,可得△ACB是直角三角形,知∠6与∠4互余,
又DE⊥AB可知∠3与∠4互余,得∠6=∠3;
②由∠6=∠3,∠3=∠2,可得∠6=∠2,从而可知tan∠6=m;
③在Rt△ACB中,由$tan∠6=\frac{BC}{AC}=m$,可设AC=x,BC=mx,
由勾股定理,得x2+(mx)2=102,可解得x的值;
④由BC=mx,可求BC的长.
点评 本题考查切线的性质、垂径定理、解直角三角形、锐角三角函数等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题,属于中考常考题型.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
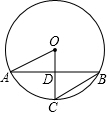 如图,⊙O的半径OC垂直于弦AB,垂足为D,OA=2$\sqrt{2}$,∠B=22.5°,AB的长为( )
如图,⊙O的半径OC垂直于弦AB,垂足为D,OA=2$\sqrt{2}$,∠B=22.5°,AB的长为( )| A. | 2 | B. | 4 | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ②④ | B. | ①③④ | C. | ①③ | D. | ①④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
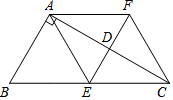 如图,在△ABC中,∠BAC=90°,线段AC的垂直平分线交AC于D点,交BC于E点,过点A作BC的平行线交直线ED于F点,连接AE,CF.
如图,在△ABC中,∠BAC=90°,线段AC的垂直平分线交AC于D点,交BC于E点,过点A作BC的平行线交直线ED于F点,连接AE,CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
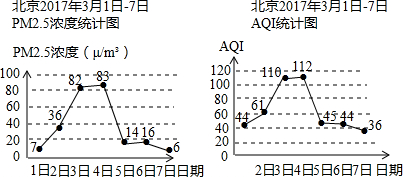
 高铁的开通,给N市市民出行带来了极大的方便,“元旦”期间,甲、乙两人应邀到A市的艺术馆参加演出,甲乘私家车从N市出发1小时后,乙乘坐高铁从N市出发,先到A市火车站,然后再转乘出租车到A市的艺术馆(换车时间忽略不计),两人恰好同时到达A市的艺术馆,他们离开N市的距离y(千米)与乘车时间x(小时)的关系如图所示,请结合图象解答下列问题:
高铁的开通,给N市市民出行带来了极大的方便,“元旦”期间,甲、乙两人应邀到A市的艺术馆参加演出,甲乘私家车从N市出发1小时后,乙乘坐高铁从N市出发,先到A市火车站,然后再转乘出租车到A市的艺术馆(换车时间忽略不计),两人恰好同时到达A市的艺术馆,他们离开N市的距离y(千米)与乘车时间x(小时)的关系如图所示,请结合图象解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com