
【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=﹣1,且过点(﹣3,0),下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(3,y2)是抛物线上两点,则y1<y2,其中说法正确的是( )
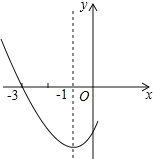
A.①②B.②③C.①②④D.②③④
【答案】A
【解析】
根据抛物线开口方向得到a>0,根据抛物线的对称轴得b=2a>0,则2a﹣b=0,则可对②进行判断:根据抛物线与y轴的交点在x轴下方得到c<0,则abc<0,于是可对①进行判断,由于x=2时,y>0,则得到4a+2b+c>0,则可对③进行判断,通过点(﹣5,y1)和点(3,y2)离对称轴的远近对④进行判断.
解:∵抛物线开口向上,
∴a>0,
∵抛物线对称轴为直线x=﹣![]() =﹣1,
=﹣1,
∴b=2a>0,则2a﹣b=0,所以②正确;
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc<0,所以①正确;
∵x=2时,y>0,
∴4a+2b+c>0,所以③错误;
∵点(﹣5,y1)离对称轴的距离与点(3,y2)离对称轴的距离相等,
∴y1=y2,所以④不正确.
故选A.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某超市平时每天都将一定数量的白糖和红糖进行包装以便出售,已知每天包装白糖的质量是包装红糖质量的![]() 倍,且每天包装白糖和红糖的质量之和为45千克.
倍,且每天包装白糖和红糖的质量之和为45千克.
(1)求平均每天包装白糖和红糖的质量各是多少千克?
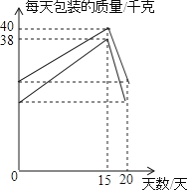
(2)为迎接今年6月25日的“端午节”,该超市决定在前20天增加每天包装白糖和红糖的质量,二者的包装质量与天数的变化情况如图所示,节日后又恢复到原来每天的包装质量.直接写出在这20天内每天包装白糖和红糖的质量随天数变化的函数关系式,并写出自变量的取值范围.
(3)假设该超市每天都会将当天包装后的白糖和红糖全部售出,已知白糖的成本价为每千克3.9元,红糖的成本每千克5.5元,二者包装费用平均每千克均为0.5元,白糖售价为每千克6元,红糖售价为每千克8元,那么在这20天中有哪几天销售白糖和红糖的利润之和大于120元?[总利润=售价额﹣成本﹣包装费用].
查看答案和解析>>
科目:初中数学 来源: 题型:
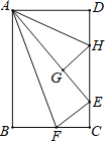
【题目】在数学拓展课《折叠矩形纸片》上,小林折叠矩形纸片ABCD进行如下操作:①把△ABF翻折,点B落在CD边上的点E处,折痕AF交BC边于点F;②把△ADH翻折,点D落在AE边长的点G处,折痕AH交CD边于点H.若AD=6,AB=10,则![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
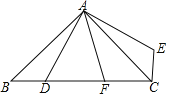
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,点D是BC上一动点,连接AD,过点A作AE⊥AD,并且始终保持AE=AD,连接CE.
(1)求证:△ABD≌△ACE;
(2)若AF平分∠DAE交BC于F,探究线段BD,DF,FC之间的数量关系,并证明;
(3)在(2)的条件下,若BD=3,CF=4,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“低碳生活,绿色出行”理念的普及,新能源汽车正逐渐成为人们喜爱的交通工具.某汽车销售公司计划购进一批新能源汽车尝试进行销售,据了解2辆A型汽车、3辆B型汽气车的进价共计80万元;3辆A型汽车、2辆B型汽车的进价共计95万元.
(1)求A、B两种型号的汽车每辆进价分别为多少方元?
(2)若该公司计划正好用200万元购进以上两种型号的新能源汽车(两种型号的汽车均购买),请你帮助该公司设计购买方案
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一期间,某商场计划购进甲、乙两种商品,已知购进甲商品1件和乙商品3件共需240元;购进甲商品2件和乙商品1件共需130元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
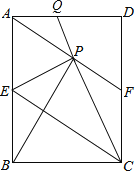
【题目】如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点,连结CP并延长CP交AD于Q点.给出以下结论:
①四边形AECF为平行四边形;
②∠PBA=∠APQ;
③△FPC为等腰三角形;
④△APB≌△EPC.
其中正确结论的个数为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y1=ax2﹣![]() x+c与x轴交于点A和点B(1,0),与y轴交于点C(0,
x+c与x轴交于点A和点B(1,0),与y轴交于点C(0,![]() ),抛物线y1的顶点为G,GM⊥x轴于点M.将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2.
),抛物线y1的顶点为G,GM⊥x轴于点M.将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2.
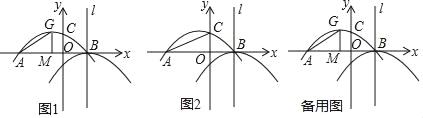
(1)求抛物线y2的解析式;
(2)如图2,在直线l上是否存在点T,使△TAC是等腰三角形?若存在,请求出所有点T的坐标;若不存在,请说明理由;
(3)点P为抛物线y1上一动点,过点P作y轴的平行线交抛物线y2于点Q,点Q关于直线l的对称点为R,若以P,Q,R为顶点的三角形与△AMG全等,求直线PR的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:如何将一个长为17,宽为1的长方形经过剪一剪,拼一拼,形成一个正方形.(下列所有图中每个小方格的边长都为1,剪拼过程中材料均无剩余)
问题探究:我们从长为5,宽为1的长方形入手.
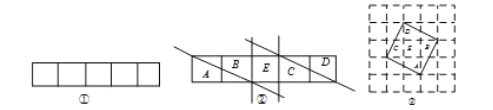
(1)如图①是一个长为5,宽为1的长方形.把这个长方形剪一剪、拼一拼后形成正方形,则正方形的面积应为_____________,设正方形的边长为![]() ,则
,则![]() _________;
_________;
(2)我们可以把有些带根号的无理数的被开方数表示成两个正整数平方和的形式,比如![]() .类比此,可以将(1)中的
.类比此,可以将(1)中的![]() 表示成
表示成![]() _____________;
_____________;
(3)![]() 的几何意义可以理解为:以长度2和3为直角边的直角三角形的斜边长为
的几何意义可以理解为:以长度2和3为直角边的直角三角形的斜边长为![]() ;类比此,(2)中的
;类比此,(2)中的![]() 可以理解为以长度________和__________为直角边的直角三角形斜边的长;
可以理解为以长度________和__________为直角边的直角三角形斜边的长;
(4)剪一剪:由(3)可画出如图②的分割线,把长方形分成![]() 五部分;
五部分;
(5)拼一拼:把图②中五部分拼接得到如图③的正方形;
问题解决:仿照上面的探究方法请把图④中长为17,宽为1的长方形剪一剪,在图⑤中画出拼成的正方形.(说明:图④的分割过程不作评分要求,只对图⑤中画出的最终结果评分)
![]()

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com