
【题目】(1)一种圆环甲(如图1),它的外圆直径是8厘米,环宽1厘米。
①如果把这样的2个圆环扣在一起并拉紧(如图2),长度为 厘米;
②如果用n个这样的圆环相扣并拉紧,长度为 厘米。
(2)另一种圆环乙,像(1)中圆环甲那样相扣并拉紧,
①3个圆环乙的长度是28cm,5个圆环乙的长度是44cm,求出圆环乙的外圆直径和环宽;
②现有n(n>2)个圆环甲和n(n>2)个圆环乙,将它们像(1)中那样相扣并拉紧,长度用n的代数式表示为多少厘米?

【答案】(1) ①14 ② 6n+2(2) 圆环乙的外圆直径为12cm,环宽为2cm②14n+3
【解析】
解:(1)①14 ② 6n+2 ……………4分
(2)①设圆环乙的外圆直径为xcm,环宽为ycm,则根据题意得:
![]() 解之得
解之得![]() ……………8分
……………8分
答:圆环乙的外圆直径为12cm,环宽为2cm. ……………9分
② ∵n个圆环甲的长度=6n+2
∴n个圆环乙的长度=8n+4
∴n个圆环甲+n个圆环乙=6n+2+8n+4-(1+2)="14n+3"
……………12分
(1)由于圆环的外圆直径是8厘米,环宽1厘米,所以内圆直径是6厘米.
①如果把这样的2个圆环扣在一起并拉紧,那么长度为2个内圆直径+2个环宽;
②如果用n个这样的圆环相扣并拉紧,那么长度为n个内圆直径+2个环宽;
(2)①根据设圆环乙的外圆直径为xcm,环宽为ycm,利用3个圆环乙的长度是28cm,5个圆环乙的长度是44cm,分别得出方程即可求出;
②首先假设总共2n个环相扣,且两头的两个也相扣,即2n个小环相扣后构成一个大环,则总长为(12+8)n-(2+4)n=14n进而分析即可.


科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AC与BD相交于点O,∠AOB=60°,BD=4,将△ABC沿直线AC翻折后,点B落在点E处,那么S△AED=______

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣2x+2与x轴、y轴分别交于A、B两点,△BAC为等腰直角三角形,且∠BAC=90°.若点C恰好落在函数y= ![]() (x>0)在第一象限内的图象上,则k的值为( )
(x>0)在第一象限内的图象上,则k的值为( )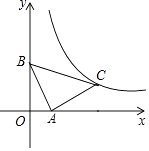
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点F在AD上,点E在BC上,把这个矩形沿EF折叠后,使点D恰好落在BC边上的G点处,若矩形面积为4 ![]() 且∠AFG=60°,GE=2BG,则折痕EF的长为( )
且∠AFG=60°,GE=2BG,则折痕EF的长为( ) 
A.1
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D、E、F分在AB、BC、AC上,且DE∥AC,EF∥AB,下面写出了证明“∠A+∠B+∠C=180°”的过程,请补充完整:
证明:∵DE∥AC,EF∥AB
∴∠1=∠ ,∠3=∠ ,( )
∵AB∥EF(已知)
∴∠2=∠ ( )
∵DE∥AC(已知)
∴∠4=∠ ( )
∴∠2=∠A( )
∵∠1+∠2+∠3=180°(平角定义)
∴∠A+∠B+∠C=180°(等量代换)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)请画出△ABC关于原点O成中心对称的图形△A2B2C2;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A表示-5,点B表示10.动点P从点A出发,沿数轴正方向以每秒1个单位的速度匀速运动;同时,动点Q从点B出发,沿数轴负方向以每秒2个单位的速度匀速运动.设运动时间为t秒.
(1)当t为 秒时,P,Q两点相遇,求出相遇点所对应的数;
(2)当t为何值时,P,Q两点的距离为3个单位长度,并求出此时点P对应的数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点).有下列结论: ①当x=3时,y=0;
②3a+b>0;
③﹣1≤a≤﹣ ![]() ;
;
④ ![]() ≤n≤4.
≤n≤4.
其中正确的有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com