
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 判定一个二次根式是不是最简二次根式的方法,就是逐个检查最简二次根式的两个条件是否同时满足,同时满足的就是最简二次根式,否则就不是.
解答 解:∵$\sqrt{{n}^{2}+2n+1}$=$\sqrt{(n+1)^{2}}$=|n+1|,$\sqrt{12}$=2$\sqrt{3}$,
∴$\sqrt{{n}^{2}+2n+1}$和$\sqrt{12}$不是最简二次根式,
∴最简二次根式有$\sqrt{2a}$、$\sqrt{1+a}$、$\sqrt{{a}^{2}+{b}^{2}}$、$\sqrt{10}$.
故选C.
点评 本题考查最简二次根式的定义.根据最简二次根式的定义,最简二次根式必须满足两个条件:被开方数不含分母;被开方数不含能开得尽方的因数或因式.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:填空题
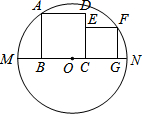 如图,两个正方形都在⊙O的直径MN的同侧,顶点B、C、G都在MN上,正方形ABCD的顶点A和正方形CEFG的顶点F都在⊙O上,点E在CD上.若AB=5,FG=3,则OC的长为2.
如图,两个正方形都在⊙O的直径MN的同侧,顶点B、C、G都在MN上,正方形ABCD的顶点A和正方形CEFG的顶点F都在⊙O上,点E在CD上.若AB=5,FG=3,则OC的长为2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
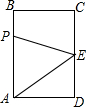 如图,长方形ABCD中,AB=4cm,BC=3cm,E为CD的中点.动点P从A点出发,以每秒1cm的速度沿A-B-C-E运动,最终到达点E.若点P运动的时间为x秒,则当x=$\frac{10}{3}$或5时,△APE的面积等于5.
如图,长方形ABCD中,AB=4cm,BC=3cm,E为CD的中点.动点P从A点出发,以每秒1cm的速度沿A-B-C-E运动,最终到达点E.若点P运动的时间为x秒,则当x=$\frac{10}{3}$或5时,△APE的面积等于5.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
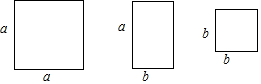
| A. | a+b | B. | 2a+b | C. | 2a-b | D. | a+2b |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
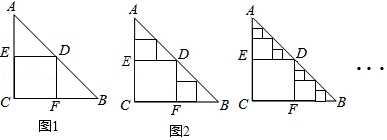
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com