
分析 (1)先把各二次根式化简为最简二次根式,然后合并后进行二次根式的乘法运算;
(2)先把各二次根式化简为最简二次根式,然后进行二次根式的除法运算;
(3)利用平方差公式和完全平方公式计算;
(4)先分母有理化,再进行乘法运算,然后合并即可.
解答 解:(1)原式=(5$\sqrt{2}$-8$\sqrt{2}$)×$\sqrt{3}$-$\sqrt{6}$
=-3$\sqrt{6}$-$\sqrt{6}$
=-4$\sqrt{6}$;
(2)原式=(9$\sqrt{2}$+$\sqrt{2}$-2$\sqrt{2}$)÷4$\sqrt{2}$
=8$\sqrt{2}$÷4$\sqrt{2}$
=2;
(3)原式=4-6-(3-2+$\frac{1}{3}$)
=-2-$\frac{4}{3}$
=-$\frac{10}{3}$;
(4)原式=$\sqrt{2}$+1+3-3$\sqrt{2}$+2$\sqrt{2}$
=4.
点评 本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.


科目:初中数学 来源: 题型:解答题
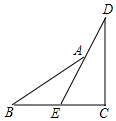 如图,阅读下面的题目及分析过程,并按要求进行证明.
如图,阅读下面的题目及分析过程,并按要求进行证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,圆柱形容器中,高为18cm,底面周长为24cm,在容器内壁离容器底部4cm的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿2cm与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为0.2m(容器厚度忽略不计).
如图,圆柱形容器中,高为18cm,底面周长为24cm,在容器内壁离容器底部4cm的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿2cm与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为0.2m(容器厚度忽略不计).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知二次函数y1=ax2+bx+c的图象过点A(1,0),B(-3,0),C(0,-3)
如图,已知二次函数y1=ax2+bx+c的图象过点A(1,0),B(-3,0),C(0,-3)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
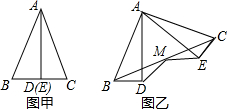 已知:如图甲,用顶角平分线将等腰三角形△ABC分成两个全等的三角形,若将△ABD保持不动,△AEC绕点A逆时针旋转到如图乙的位置,连接BC,取BC的中点M,连接MD,ME,求证:MD=ME.
已知:如图甲,用顶角平分线将等腰三角形△ABC分成两个全等的三角形,若将△ABD保持不动,△AEC绕点A逆时针旋转到如图乙的位置,连接BC,取BC的中点M,连接MD,ME,求证:MD=ME.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com