
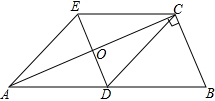
 如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA和BC的平行线,两线交于点E,且DE交AC于点O,连接AE.
如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA和BC的平行线,两线交于点E,且DE交AC于点O,连接AE.分析 (1)欲证明四边形ADCE是菱形,需先证明四边形ADCE为平行四边形,然后再证明其对角线相互垂直;
(2)根据勾股定理得到AC的长度,由含30度角的直角三角形的性质求得DE的长度,然后由菱形的面积公式:S=$\frac{1}{2}$AC•DE进行解答.
解答 (1)证明:∵DE∥BC,EC∥AB,
∴四边形DBCE是平行四边形.
∴EC∥DB,且EC=DB.
在Rt△ABC中,CD为AB边上的中线,
∴AD=DB=CD.
∴EC=AD.
∴四边形ADCE是平行四边形.
∴ED∥BC.
∴∠AOD=∠ACB.
∵∠ACB=90°,
∴∠AOD=∠ACB=90°.
∴平行四边形ADCE是菱形;
(2)解:Rt△ABC中,CD为AB边上的中线,∠B=60°,BC=6,
∴AD=DB=CD=6.
∴AB=12,由勾股定理得$AC=6\sqrt{3}$.
∵四边形DBCE是平行四边形,
∴DE=BC=6.
∴${S_{菱形ADCE}}=\frac{AC•ED}{2}=\frac{{6\sqrt{3}×6}}{2}=18\sqrt{3}$.
点评 此题主要考查菱形的性质和判定以及面积的计算,使学生能够灵活运用菱形知识解决有关问题.


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:选择题
| A. | a1=a2 | B. | a1=-a2 | C. | a1=±a2 | D. | 无法判断 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD是平行四边形,点A(1,0),B(3,1),C(3,3),反比例函数y=$\frac{m}{x}$(x>0)的图象过点D,点P是一次函数y=kx+3-3k(k≠0)的图象与该反比例函数的一个公共点.对于一次函数y=kx+3-3k(k≠0),当y随x的增大而增大时,则点P横坐标a的取值范围$\frac{2}{3}$<a<3.
如图,四边形ABCD是平行四边形,点A(1,0),B(3,1),C(3,3),反比例函数y=$\frac{m}{x}$(x>0)的图象过点D,点P是一次函数y=kx+3-3k(k≠0)的图象与该反比例函数的一个公共点.对于一次函数y=kx+3-3k(k≠0),当y随x的增大而增大时,则点P横坐标a的取值范围$\frac{2}{3}$<a<3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 鞋的尺码(单位:cm) | 23.5 | 24 | 24.5 | 25 | 26 |
| 销售量(单位:双) | 1 | 2 | 2 | 5 | 1 |
| A. | 25,24.5 | B. | 24.5,25 | C. | 26,25 | D. | 25,25 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | p>2 | B. | p>0 | C. | p≤2 | D. | 0<p≤2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
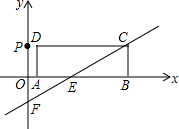 已知长方形ABCD的边长AB=9,AD=3,现将此长方形置于平面直角坐标系中,使AB在x轴的正半轴上,经过点C的直线y=$\frac{1}{2}$x-2与x轴交于点E,与y轴交于点F.
已知长方形ABCD的边长AB=9,AD=3,现将此长方形置于平面直角坐标系中,使AB在x轴的正半轴上,经过点C的直线y=$\frac{1}{2}$x-2与x轴交于点E,与y轴交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com