
科目:初中数学 来源: 题型:解答题
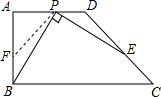 下面是一个研究性解题案例,请补充完整:
下面是一个研究性解题案例,请补充完整:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:在平面直角坐标系中,A(0,1),B(2,0),C(4,3)
已知:在平面直角坐标系中,A(0,1),B(2,0),C(4,3)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
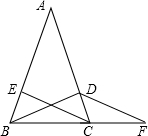 推理填空
推理填空查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 2016年3月31日晚,王凯同学来到金熊国际影城看电影,进场时,发现门票还在家里,此时距离电影播放还有20分钟,于是他立即步行回家取票,同时他爸爸从家里骑自行车以王凯3倍的速度给他送票,两人在途中相遇后,爸爸立即骑自行车送王凯去金熊国际影城.如图表示的是王凯和他爸爸距离金熊国际影城的距离y(米)与时间x(分钟)之间的函数关系的图象(不完整).
2016年3月31日晚,王凯同学来到金熊国际影城看电影,进场时,发现门票还在家里,此时距离电影播放还有20分钟,于是他立即步行回家取票,同时他爸爸从家里骑自行车以王凯3倍的速度给他送票,两人在途中相遇后,爸爸立即骑自行车送王凯去金熊国际影城.如图表示的是王凯和他爸爸距离金熊国际影城的距离y(米)与时间x(分钟)之间的函数关系的图象(不完整).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com