
【题目】如图,点E在△ABC的边AB上,过点B,C,E的⊙O切AC于点C.直径CD交BE于点F,连结BD,DE.已知∠A=∠CDE,AC=2![]() ,BD=1.
,BD=1.
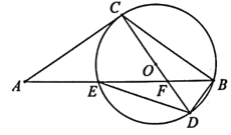
(1)求⊙O的直径.
(2)过点F作FG⊥CD交BC于点G,求FG的长.
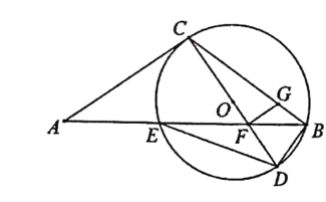
【答案】(1)3;(2)![]()
【解析】
(1)因为CD是⊙O的直径,所以∠CBD=90°,因为∠A=∠CDE=∠CBA,可得BC=AC=2![]() ,因为BD=1,在Rt△CBD中,用勾股定理即可得出⊙O的直径;
,因为BD=1,在Rt△CBD中,用勾股定理即可得出⊙O的直径;
(2)由题意,可得FG∥AC,所以∠GFB=∠CAB=∠CBA,即FG=GB=x,根据sin∠BCD=![]() ,得CG=3FG=3x,由BC=2
,得CG=3FG=3x,由BC=2![]() 可列方程:x+3x=2
可列方程:x+3x=2![]() ,解得x的值即可得出FG的长.
,解得x的值即可得出FG的长.
(1)∵CD是⊙O的直径,
∴∠CBD=90°,
∵∠A=∠CDE,∠CDE=∠CBA,
∴∠CAB=∠CBA,
∴BC=AC=2![]() ,
,
∵BD=1,
∴⊙O的直径CD=![]() ;
;
(2)如图,∵过点B,C,E的圆O切AC于点C,直径CD交BE于点F,
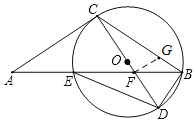
∴AC⊥CD,
∵FG⊥CD,
∴FG∥AC,
∴∠GFB=∠CAB=∠CBA,
∴FG=GB=x,
∵sin∠BCD=![]() ,
,
∴![]() ,即CG=3FG=3x,
,即CG=3FG=3x,
∵BC=2![]() ,
,
∴x+3x=2![]() ,
,
∴FG=x=![]() .
.


科目:初中数学 来源: 题型:
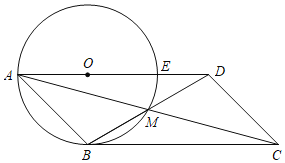
【题目】平行四边形ABCD的对角线相交于点M,△ABM的外接圆交AD于点E且圆心O恰好落在AD边上,连接ME,若∠BCD=45°
(1)求证:BC为⊙O切线;
(2)求∠ADB的度数;
(3)若ME=1,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防疾病,某单位对办公室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成为正比例,药物燃烧后,y与x成反比例(如图),现测得药物8分钟燃毕,此时室内空气中每立方米的含药量6毫克,请根据题中所提供的信息,解答下列问题:

(1)药物燃烧时,y关于x的函数关系式为________,自变量x的取值范为________;药物燃烧后,y关于x的函数关系式为________.
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时员工方可进办公室,那么从消毒开始,至少需要经过________分钟后,员工才能回到办公室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“足球运球”被列入中招体育必考项目.为此某学校举行“足球运球”达标测试,将成绩10分、9分、8分、7分,对应定为A,B,C,D四个等级.某班根据测试成绩绘制如下统计图,请回答下列问题:
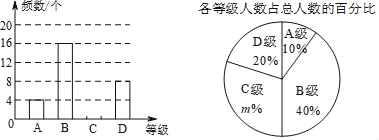
(1)该班级的总人数为 ,m= .
(2)补全条形统计图.
(3)该班“足球运球”测试的平均成绩是多少?
(4)现准备从等级为A的4个人(2男2女)中随机抽取两个人去参加比赛,请用列表或画树状图的方法,求出恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
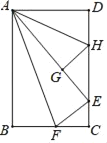
【题目】在数学拓展课《折叠矩形纸片》上,小林折叠矩形纸片ABCD进行如下操作:①把△ABF翻折,点B落在CD边上的点E处,折痕AF交BC边于点F;②把△ADH翻折,点D落在AE边长的点G处,折痕AH交CD边于点H.若AD=6,AB=10,则![]() 的值是( )
的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把长方形纸片ABCD沿对角线折叠,设重叠部分为△EBD,那么,有下列说法:①△EBD是等腰三角形,EB=ED;②折叠后∠ABE和∠CBD一定相等;③折叠后得到的图形是轴对称图形;④△EBA和△EDC一定是全等三角形.其中正确的是( )

A. ①②③B. ①③④C. ①②④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
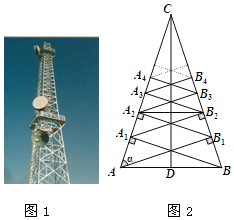
【题目】移动通信公司建设的钢架信号塔(如图1),它的一个侧面的示意图(如图2).CD是等腰三角形ABC底边上的高,分别过点A、点B作两腰的垂线段,垂足分别为B1,A1,再过A1,B1分别作两腰的垂线段所得的垂足为B2,A2,用同样的作法依次得到垂足B3,A3,….若AB为3米,sinα=![]() ,则水平钢条A2B2的长度为( )
,则水平钢条A2B2的长度为( )
A. ![]() 米B. 2米C.
米B. 2米C. ![]() 米D.
米D. ![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(
的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(![]() ,﹣2);⑤当x<
,﹣2);⑤当x<![]() 时,y随x的增大而减小;⑥a+b+c>0正确的有( )
时,y随x的增大而减小;⑥a+b+c>0正确的有( )

A. 3个 B. 4个 C. 5个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地之间有一条笔直的公路L,小明从甲地出发沿公路ι步行前往乙地,同时小亮从乙地出发沿公路L骑自行车前往甲地,小亮到达甲地停留一段时间,原路原速返回,追上小明后两人一起步行到乙地.设小明与甲地的距离为y1米,小亮与甲地的距离为y2米,小明与小亮之间的距离为s米,小明行走的时间为x分钟.y1、y2与x之间的函数图象如图1,s与x之间的函数图象(部分)如图2.
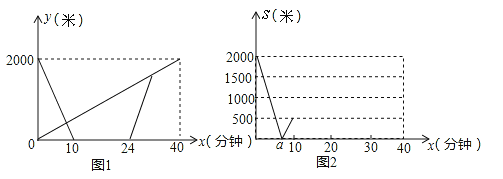
(1)求小亮从乙地到甲地过程中y1(米)与x(分钟)之间的函数关系式;
(2)求小亮从甲地返回到与小明相遇的过程中s(米)与x(分钟)之间的函数关系式;
(3)在图2中,补全整个过程中s(米)与x(分钟)之间的函数图象,并确定a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com