
分析 (1)求单价,总价已知,应根据数量来列等量关系.关键描述语是:“苹果数量是试销时的2倍”;等量关系为:2×试销时的数量=本次数量.
(2)根据盈利=(售价-进价)×销量进行计算.
解答 解:(1)设试销时这种苹果的进货价是每千克x元.
依题意,得:$\frac{13200}{x+0.5}$=$\frac{6000}{x}$×2,
解之得:x=5,
经检验:x=5是原方程的解.
∴x=5.
答:试销时该品种苹果的进货价是每千克5元;
(2)(7-5)×$\frac{6000}{5}$×3=7200(元).
点评 本题考查分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:解答题
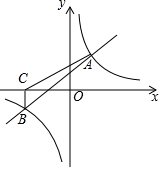 如图,一次函数y=x+2与反比例函数y=$\frac{k}{x}$的图象相交于A(2,m),B(-4,n)两点.
如图,一次函数y=x+2与反比例函数y=$\frac{k}{x}$的图象相交于A(2,m),B(-4,n)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
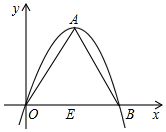 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
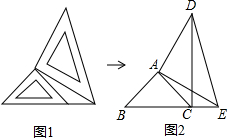 如图,两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.请找出图2中的全等三角形,并给予证明(不再添加其它线段,不再标注或使用其它字母).
如图,两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.请找出图2中的全等三角形,并给予证明(不再添加其它线段,不再标注或使用其它字母).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
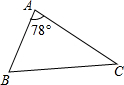 如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )| A. | 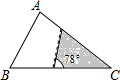 | B. |  | C. | 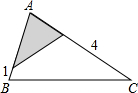 | D. | 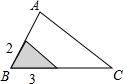 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com