
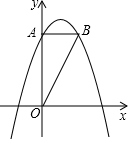
 如图,已知抛物线y=ax2+bx+4经过点(2,4),(-2,-2),交y轴于点A,过点A作AB⊥y轴交抛物线于点B.
如图,已知抛物线y=ax2+bx+4经过点(2,4),(-2,-2),交y轴于点A,过点A作AB⊥y轴交抛物线于点B.分析 (1)直接利用已知点代入函数解析式进而得出答案;
(2)利用已知得出A,B点坐标,再利用旋转的性质得出B′点坐标,进而判断得出答案.
解答 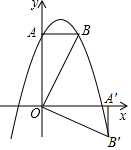 解:(1)将点(2,4),(-2,-2),代入函数解析式得:
解:(1)将点(2,4),(-2,-2),代入函数解析式得:
$\left\{\begin{array}{l}{4a+2b+4=4}\\{4a-2b+4=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{3}{4}}\\{b=\frac{3}{2}}\end{array}\right.$,
故抛物线解析式为:y=-$\frac{3}{4}$x2+$\frac{3}{2}$x+4;
(2)B'落在抛物线上,
理由:∵抛物线与y轴于点A,
∴x=0时,y=4,即A(0,4),
当y=4时,4=-$\frac{3}{4}$x2+$\frac{3}{2}$x+4,
解得:x1=0,x2=2,
∴B(2,4),
∵将△OAB绕点O顺时针旋转90°得到△OA'B',
∴B′(4,-2),
当x=4时,-$\frac{3}{4}$×16+$\frac{3}{2}$×4+4=-2,
故B'落在抛物线上.
点评 此题主要考查了待定系数法求二次函数解析式以及旋转的性质,正确得出B′点坐标是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
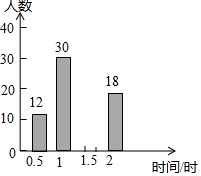 在西安市开展“美丽城市,创卫同行”活动中,我校倡议七年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制不完整的统计图表,如图所示:
在西安市开展“美丽城市,创卫同行”活动中,我校倡议七年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制不完整的统计图表,如图所示:| 劳动时间(时)0.5 | 频数(人数)12 | 频率0.12 |
| 1 | 30 | 0.3 |
| 1.5 | x | 0.4 |
| 2 | 18 | y |
| 合计 | m | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
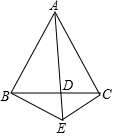 如图,在△ABC中,AB=AC,AD平分∠BAC,E是AD的延长线上任意一点,连接BE,CE.则四边形ABEC是轴对称图形吗?请简单说明理由.
如图,在△ABC中,AB=AC,AD平分∠BAC,E是AD的延长线上任意一点,连接BE,CE.则四边形ABEC是轴对称图形吗?请简单说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
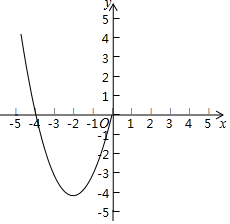 某数学兴趣小组对函数y=x2-4|x|的图象和性质进行探究,发现自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
某数学兴趣小组对函数y=x2-4|x|的图象和性质进行探究,发现自变量x的取值范围是全体实数,x与y的几组对应值列表如下:| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | … | -3 | -4 | -3 | 0 | -3 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
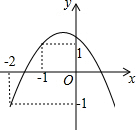 如图,已知关于x的二次函数y=ax2+bx+c的图象经过点(-2,y1),(-1,y2),(1,0),且y1<0<y2,对于以下结论:①abc>0;②a+3b+2c≤0;③a<-$\frac{1}{2}$c;④在-2<x<-1中存在一个实数x0,使得x0=-$\frac{a+b}{a}$,其中正确的个数有( )
如图,已知关于x的二次函数y=ax2+bx+c的图象经过点(-2,y1),(-1,y2),(1,0),且y1<0<y2,对于以下结论:①abc>0;②a+3b+2c≤0;③a<-$\frac{1}{2}$c;④在-2<x<-1中存在一个实数x0,使得x0=-$\frac{a+b}{a}$,其中正确的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
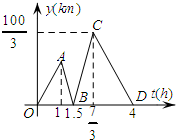 甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图所示,已知乙比甲先出发1h.
甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图所示,已知乙比甲先出发1h.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com