
【题目】现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)从中任取一张,求取到偶数的概率.
(2)甲、乙两人进行摸牌游戏.
①甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
②若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②甲获胜的概率大,游戏不公平,见解析;
;②甲获胜的概率大,游戏不公平,见解析;
【解析】
(1)属于求简单事件的概率,根据概率公式计算可得;
(2)用列表格法列出所有的等可能结果,①从中得到两数字相同的结果数,利用概率公式计算;②从中得到和为2的倍数和和为5的倍数的结果数,利用概率公式计算和为2的倍数和和为5的倍数的概率,则可得甲获胜和乙获胜的概率,比较结果判断游戏是否公平.
解:(1)从中任取一张,共有3种等可能结果,分别为2,3,5,其中偶数有1种,为2,所以任取一张是偶数的概率为P=![]()
(2)游戏不公平,理由如下:
用列表法表示所有可能出现的结果如图:
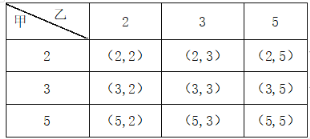
①从表格可以看出,总共有9种结果,每种结果出现的可能性相同,其中两数字相同的有3种,分别为(2,2),(3,3),(5,5),所以两人抽取相同数字的概率为P=![]() ;
;
②从表格可以看出,总共有9种结果,每种结果出现的可能性相同,其中两人抽取数字和为2的倍数有5种,分别是(2,2),(3,3),(3,5),(5,3),(5,5),所以甲获胜的概率是P(甲获胜)=![]() ,两人抽取数字和为5的倍数有3种,分别是(2,3),(3,2),(5,5),所以乙获胜的概率是P(乙获胜)=
,两人抽取数字和为5的倍数有3种,分别是(2,3),(3,2),(5,5),所以乙获胜的概率是P(乙获胜)= ![]() ,∵
,∵![]() ,所以甲获胜的概率大,游戏不公平.
,所以甲获胜的概率大,游戏不公平.


科目:初中数学 来源: 题型:
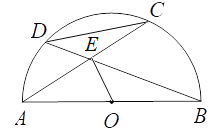
【题目】如图,以AB为直径的半圆O内有一条弦AC,点E是弦AC的中点,连接BE,并延长交半圆O于点D,若OB=2,OE=1,则∠CDE的度数是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:三角形的角平分线是初中几何中一条非常重要的线段,它除了具有平分角、角平分线上的点到角两边的距离相等这些性质外,还具有以下的性质:
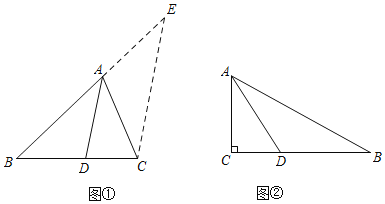
如图①,在△ABC中,AD平分∠BAC交BC于点D,则![]() =
=![]() .提示:过点C作CE∥AD交BA的延长线于点E.
.提示:过点C作CE∥AD交BA的延长线于点E.
请根据上面的提示,写出得到“![]() ”这一结论完整的证明过程.
”这一结论完整的证明过程.
结论应用:如图②,在Rt△ABC中,∠C=90°,AC=8,BC=15,AD平分∠BAC交BC于点D.请直接利用“问题探究”的结论,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B两点的坐标分别为(4,0)和(0,3),动点P从点A出发,以每秒2个长度单位的速度沿AO向O运动,在点P出发的同时,动直线EF从x轴出发,以每秒1个长度单位沿y轴方向向上平移,分别与y轴、线段AB交于EP、FP.设运动时间为ts(0<t≤2).
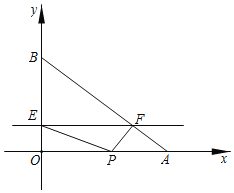
(1)在运动过程中,是否存在某一时刻t,使得△EOP与△AOB相似?若存在,请求出所有符合题意的t的值;若不存在,请说明理由.
(2)若△PEF是等腰三角形,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在矩形ABCD中,AB=8,BC=x(0<x≤8),点E在边CD上,且CE=CB,以AE为对角线作正方形AGEF.设正方形AGEF的面积y.
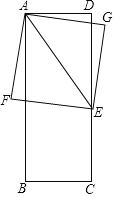
(1)当点F在矩形ABCD的边上时,x= .
(2)求y与x的函数关系式及y的取值范围.
(3)当矩形ABCD的一条边将正方形AGEF的面积分为1:3两部分时,直接写出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)与x轴的一个交点坐标为(2,0),对称轴是直线x=1,其图象的一部分如图所示,对于下列说法:其中正确的是( )
①抛物线过原点:
②a﹣b+c<0:
③2a+b+c=0;
④抛物线顶点为(1,![]() ):
):
⑤当x<1时,y随x的增大而增大
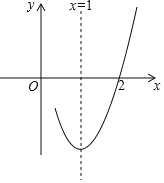
A.①②③B.①③④C.①④⑤D.③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线L:y=ax2+bx+c(a≠0)与x轴交于A、B两点.与y轴交于C点.且A(﹣1,0),OB=OC=3OA.

(1)求抛物线L的函数表达式;
(2)在抛物线L的对称轴上是否存在一点M,使△ACM周长最小?若存在,求出点M的坐标;若不存在,请说明理由.
(3)连接AC、BC,在抛物线L上是否存在一点N,使S△ABC=2S△OCN?若存在,求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳国际马拉松赛事设有A“全程马拉松”,B“半程马拉松”,C“嘉年华马拉松”三个项目,小智和小慧参加了该赛事的志愿者服务工作,组委会将志愿者随机分配到三个项目组.
(1)小智被分配到A“全程马拉松”项目组的概率为 .
(2)用树状图或列表法求小智和小慧被分到同一个项目标组进行志愿服务的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
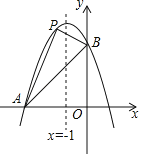
【题目】如图,已知抛物线经过两点A(﹣3,0),B(0,3),且其对称轴为直线x=﹣1.
(1)求此抛物线的解析式;
(2)若点P是抛物线上点A与点B之间的动点(不包括点A,点B),求△PAB的面积的最大值,并求出此时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com