
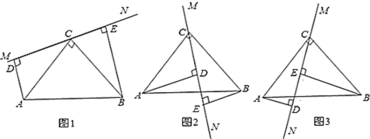
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,且
,且![]() 于点
于点![]() ,
,![]() 于点
于点![]() .易得
.易得![]() (不需要证明).
(不需要证明).
(1)当直线![]() 绕点
绕点![]() 旋转到图2的位置时,其余条件不变,你认为上述结论是否成立?若成立,写出证明过程;若不成立,请写出此时
旋转到图2的位置时,其余条件不变,你认为上述结论是否成立?若成立,写出证明过程;若不成立,请写出此时![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(2)当直线![]() 绕点
绕点![]() 旋转到图3的位置时,其余条件不变,请直接写出此时
旋转到图3的位置时,其余条件不变,请直接写出此时![]() 之间的数量关系(不需要证明).
之间的数量关系(不需要证明).
【答案】(1) 不成立,DE=AD-BE,理由见解析;(2) DE=BE-AD
【解析】
(1)DE、AD、BE之间的数量关系是DE=AD-BE.由垂直的性质可得到∠CAD=∠BCE,证得△ACD≌△CBE,得到AD=CE,CD=BE,即有DE=AD-BE;
(2)DE、AD、BE之间的关系是DE=BE-AD.证明的方法与(1)一样.
(1)不成立.
DE、AD、BE之间的数量关系是DE=AD-BE,
理由如下:如图,
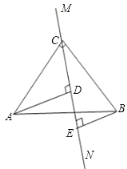
∵∠ACB=90°,BE⊥CE,AD⊥CE,![]() ,
,
∴∠ACD+∠CAD=90°,
又∠ACD+∠BCE=90°,
∴∠CAD=∠BCE,
在△ACD和△CBE中,
 ,
,
∴△ACD≌△CBE(AAS),
∴AD=CE,CD=BE,
∴DE=CE-CD=AD-BE;
(2)结论:DE=BE-AD.
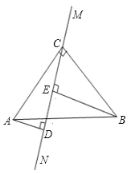
∵∠ACB=90°,BE⊥CE,AD⊥CE,![]() ,
,
∴∠ACD+∠CAD=90°,
又∠ACD+∠BCE=90°,
∴∠CAD=∠BCE,
在△ACD和△CBE中,
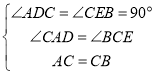 ,
,
∴△ADC≌△CEB(AAS),
∴AD=CE,DC=BE,
∴DE=CD-CE=BE-AD.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知一条直线过点(0,4),且与抛物线y=![]() x2交于A,B两点,其中点A的横坐标是-2.
x2交于A,B两点,其中点A的横坐标是-2.
(1)求这条直线的解析式及点B的坐标;
(2)在x轴上是否存在点C,使得△ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)过线段AB上一点P,作PM∥x轴,交抛物线于点M,点M在第一象限,点N(0,1),当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理神秘而美妙,它的证法多样,其中的“面积法”给了李明灵感,他惊喜地发现;当两个全等的直角三角形如图(1)摆放时可以利用面积法”来证明勾股定理,过程如下
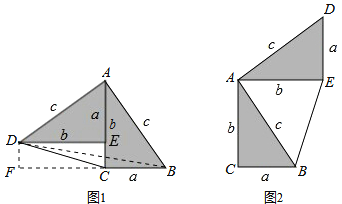
如图(1)∠DAB=90°,求证:a2+b2=c2
证明:连接DB,过点D作DF⊥BC交BC的延长线于点F,则DF=b-a
S四边形ADCB=![]()
S四边形ADCB=![]()
∴![]() 化简得:a2+b2=c2
化简得:a2+b2=c2
请参照上述证法,利用“面积法”完成如图(2)的勾股定理的证明,如图(2)中∠DAB=90°,求证:a2+b2=c2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC=2,以AB为直径的圆交BC于D,则图中阴影部分的面积为( )

A. 1 B. 2 C. 1+![]() D. 2﹣
D. 2﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
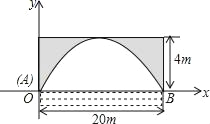
【题目】有一座抛物线形拱桥,正常水位时桥下水面宽为20m,拱顶距水面4m.
(1)在如图的直角坐标系中,求出该抛物线的解析式;
(2)为保证过往船只顺利航行,桥下水面宽度不得小于18m,求水面在正常水位基础上,最多涨多少米,不会影响过往船只?
查看答案和解析>>
科目:初中数学 来源: 题型:
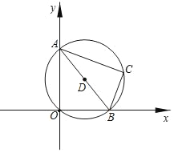
【题目】如图,在平面直角坐标系中,有一条长为10的线段AB,其端点A、点B分别在y轴、x轴上滑动,点C为以AB为直径的⊙D上一点(C始终在第一象限),且tan∠BAC=![]() .则当点A从A0(0,10)滑动到O(0,0),B从O(0,0)滑动到B0(10,0)的过程中,点C运动的路径长为_____.
.则当点A从A0(0,10)滑动到O(0,0),B从O(0,0)滑动到B0(10,0)的过程中,点C运动的路径长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
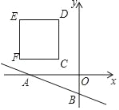
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x﹣1分别交x轴、y轴于点A、B,在第二象限内有一边长为2的正方形CDEF,已知C(﹣1,1),若动点P从C出发以每秒1个单位的速度沿着正方形CDEF的边逆时针运动一周(到达C点后停止运动),设P点运动的时间为t秒.
x﹣1分别交x轴、y轴于点A、B,在第二象限内有一边长为2的正方形CDEF,已知C(﹣1,1),若动点P从C出发以每秒1个单位的速度沿着正方形CDEF的边逆时针运动一周(到达C点后停止运动),设P点运动的时间为t秒.
(1)是否存在t,使得以P为圆心,![]() 为半径的圆与直线AB相切?若存在,求出所有t的值;若存在,请说明理由.
为半径的圆与直线AB相切?若存在,求出所有t的值;若存在,请说明理由.
(2)在点P运动的同时,直线AB以每秒1个单位的速度向右作匀速运动(与点P同时停止)是否存在t,使得以P为圆心,![]() 为半径的圆与平移后的直线A′B′相切?请直接写出所有t的值.
为半径的圆与平移后的直线A′B′相切?请直接写出所有t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】台风是一种自然灾害,它在以台风中心为圆心,一定长度为半径的圆形区域内形成极端气候,有极强的破坏力.如图,监测中心监测到一台风中心沿监测点B与监测点A所在的直线由东向西移动,已知点C为一海港,且点C与A, B两点的距离分别为300km、 400km,且∠ACB=90°,过点C作CE⊥AB于点E,以台风中心为圆心,半径为260km的圆形区域内为受影响区域.
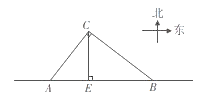
(1)求监测点A与监测点B之间的距离;
(2)请判断海港C是否会受此次台风的影响,并说明理由;
(3)若台风的速度为25km/h,则台风影响该海港多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
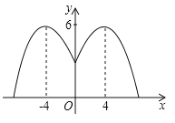
【题目】某游乐园要建一个圆形喷水池,在喷水池的中心安装一个大的喷水头,高度为![]() m,喷出的水柱沿抛物线轨迹运动(如图),在离中心水平距离4m处达到最高,高度为6m,之后落在水池边缘,那么这个喷水池的直径AB为____m.
m,喷出的水柱沿抛物线轨迹运动(如图),在离中心水平距离4m处达到最高,高度为6m,之后落在水池边缘,那么这个喷水池的直径AB为____m.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com