
 如图所示,EFGHIJKLMNPQ是正方形ABCD内部最大的正十二边形,正方形与正十二边形的边长差为6,那么正十二边形的面积是54.
如图所示,EFGHIJKLMNPQ是正方形ABCD内部最大的正十二边形,正方形与正十二边形的边长差为6,那么正十二边形的面积是54. 分析 如图,连接AC、BD交于点O,把△OAE放大,作FY⊥AE于Y,OX⊥AE于X.由题意,∠A=45°,∠AEF=30°,AE=3,设FY=a,则EY=$\sqrt{3}$a,AY=FY=a,列出方程求出a,再根据△AEF∽△AOE,得$\frac{AE}{AO}$=$\frac{AF}{AE}$,求出OA、OX,根据s△OEF=S△AEO-S△AEF,求出△OEF的面积即可解决问题.
解答 解:如图,连接AC、BD交于点O,把△OAE放大,作FY⊥AE于Y,OX⊥AE于X.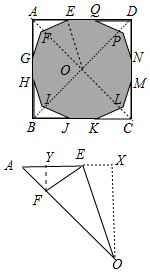
由题意,∠A=45°,∠AEF=30°,AE=3,设FY=a,则EY=$\sqrt{3}$a,AY=FY=a,
∴$\sqrt{3}$a+a=3,
∴a=$\frac{3}{2}$($\sqrt{3}$-1),AF=$\sqrt{2}$a=$\frac{3}{2}$($\sqrt{6}$-$\sqrt{2}$),
∵∠A=∠A,∠AEF=∠AOE=30°,
∴△AEF∽△AOE,
∴$\frac{AE}{AO}$=$\frac{AF}{AE}$,
∴$\frac{3}{AO}$=$\frac{\frac{3}{2}(\sqrt{6}-\sqrt{2})}{3}$,
∴OA=$\frac{3}{2}$($\sqrt{6}$+$\sqrt{2}$),
∴OX=AX=$\frac{3}{2}$($\sqrt{3}$+1),
∴s△OEF=S△AEO-S△AEF=$\frac{1}{2}$×3×$\frac{3}{2}$($\sqrt{3}+1)$-$\frac{1}{2}$×3×$\frac{3}{2}$($\sqrt{3}$-1)=$\frac{9}{2}$,
∴正十二边形的面积=12×$\frac{9}{2}$=54.
故答案为54.
点评 本题考查正多边形与圆、等腰直角三角形的性质、30度的直角三角形的性质、相似三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会用分割法求三角形面积,属于中考填空题中的压轴题.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
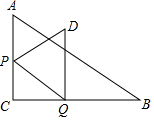 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=6,点P、Q分别在AC、BC边上,PQ∥AB.将线段PQ绕点P按逆时针方向旋转60°,得到线段PD,连接DQ.设PC=x.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=6,点P、Q分别在AC、BC边上,PQ∥AB.将线段PQ绕点P按逆时针方向旋转60°,得到线段PD,连接DQ.设PC=x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
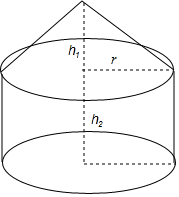 蒙古包可以近似地看作由圆锥和圆柱组成.如图,是一个蒙古包的示意图,现在想用毛毡搭建20个底面积为4πm2,高为3.5m,外围高为2m的蒙古包,至少需要多少平方米的毛毡?
蒙古包可以近似地看作由圆锥和圆柱组成.如图,是一个蒙古包的示意图,现在想用毛毡搭建20个底面积为4πm2,高为3.5m,外围高为2m的蒙古包,至少需要多少平方米的毛毡?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com