练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．如图，AB∥DE，∠B=80°，CM平分∠BCD，CN⊥CM，求∠NCE的度数．

    分析 先根据AB∥DE，得出∠B+∠DCB=180°故可得出∠DCB的度数，再根据CM平分∠BCD，可知∠DCM=$\frac{1}{2}$∠BCD，由CM⊥CN，可知∠MCN=90°，根据∠ECN=180°-∠MCN-∠DCM即可得出结论．

    解答 解：∵AB∥DE，∠B=80°
    ∴∠B+∠DCB=180°，
    ∴∠DCB=180°-80°=100°，
    ∵CM平分∠BCD，
    ∴∠DCM=$\frac{1}{2}$∠BCD=$\frac{1}{2}$×100°=50°，
    ∵CM⊥CN，
    ∴∠MCN=90°，
    ∴∠ECN=180°-90°-50°=40°．

    点评 本题考查的是平行线的性质，用到的知识点为：两直线平行，同旁内角互补．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    9．若|x-2|+（y-3）2=0，则xy=6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．【问题情境】
    如图1，四边形ABCD是正方形，M是BC边上的一点，E是CD边的中点，AE平分∠DAM．
    【探究发现】
    （1）请你判断AM、AD、MC三条线段的数量关系，并说明理由
    （2）AM=DE+BM是否成立？若成立，请给出证明；若不成立，请说明理由．
    【拓展延伸】
    （3）若四边形ABCD是长与宽不相等的矩形，其他条件不变，如图2，上述（1）、（2）中的结论是否仍然成立？请分别作出判断，不需要证明．

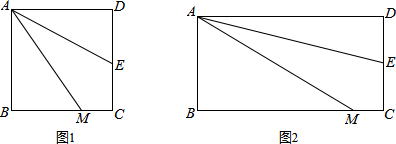
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

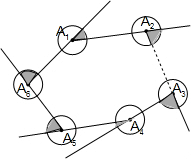    7．如图所示，分别以n边形的顶点为圆心，以1cm为半径画园，当n=2017时则图中阴影部分的面积之和为（　　）
    A．πcm2B．2πcm2C．2016πcm2D．2017πcm2

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．若$\root{3}{a}$=a，则a=0或±1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．如果要证明平行四边形ABCD为正方形，那么我们需要在四边形ABCD是平行四边形的基础上，进一步证明（　　）
    A．AC和BD互相垂直平分B．AB=AD且AC⊥BD
    C．∠A=∠B且AC=BDD．AB=AD且AC=BD

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．如果$\left\{\begin{array}{l}x=2\\ y=2\end{array}\right.$是方程组$\left\{\begin{array}{l}x+y=a\\ 2x-y=b+1\end{array}\right.$的解，则a-b=3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．某超市电器销售每台进价分别为200元、170元的A、B两种型号的电风扇，下表是近两周的销售情况：
    销售时段销售量销售收入
    A型号B型号
    第一周3台5台1800元
    第二周4台10台3100元
    （1）求A、B两种型号的电风扇的销售价．
    （2）若超市准备用不多于5400元的金额再采购这两种型号的电风扇30台，求A种型号的电风扇最多能采购多少台？
    （3）在（2）的条件下，超市销售完这30台电风扇能否实现利润为1400元的目标？若能请给出采购方案．若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，AD是△ABC的角平分线，DE，DF分别是△ABD和△ACD的高线，EF，
    AD交于点G．
    （1）求证：AE=AF；
    （2）若EF=6，AD=8，求四边形AEDF的面积．

    查看答案和解析>>

    同步练习册答案