
分析 由题目可知△>0,可求得m的值,两根之积为m2+1,为正数,可知x1,x2同号,由两根之和为负数,可知两个根一定都为负数,从而解答此题.
解答 解:(1)∵二次函数y=x2-(2m-3)x+(m2+1),其图象与x轴有两个不同交点,
∴△=[-(2m-3)]2-4×1×(m2+1),
得 m$<\frac{5}{12}$;
(2)设抛物线与x轴的交点坐标为;(x1,0),(x2,0),
∵y=0时,x2-(2m-3)x+(m2+1)=0,
∴${x}_{1}{x}_{2}={m}^{2}+1>0$,
∴x1,x2同号,
又∵x1+x2=2m-3,$m<\frac{5}{12}$,
∴x1+x2<0,
∴x1,x2都为负数,
故抛物线与x轴的交点都在x轴的负半轴上.
点评 本题考察二次函数中的△与y=0时,相应的x的值,根与系数的关系进行判断两根的正负情况.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:解答题
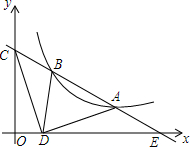 如图,已知反比例函数y=$\frac{m}{x}$与一次函数y=kx+b的图象相交于A(4,1)、B(a,2)两点,一次函数的图象与x轴、y轴的交点分别为C、E.
如图,已知反比例函数y=$\frac{m}{x}$与一次函数y=kx+b的图象相交于A(4,1)、B(a,2)两点,一次函数的图象与x轴、y轴的交点分别为C、E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
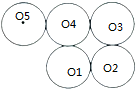 有5个半径相等的圆,排成如图所示图形,点O5是最左上方这个圆的圆心,现在要过点O5作一条直线将5个圆分成面积相等的两部分,请你根据所学知识试一试.
有5个半径相等的圆,排成如图所示图形,点O5是最左上方这个圆的圆心,现在要过点O5作一条直线将5个圆分成面积相等的两部分,请你根据所学知识试一试.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
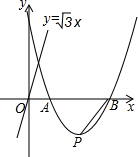 如图,抛物线y=$\frac{\sqrt{3}}{2}$x2-4$\sqrt{3}$x+6$\sqrt{3}$与x轴交于A、B,点P为顶点,在直线y=$\sqrt{3}$x上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐标,若不存在,请说明理由.
如图,抛物线y=$\frac{\sqrt{3}}{2}$x2-4$\sqrt{3}$x+6$\sqrt{3}$与x轴交于A、B,点P为顶点,在直线y=$\sqrt{3}$x上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐标,若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABC中,∠B=30°,∠C=45°,AB=2$\sqrt{3}$,点E在边AB上,点D在边BC上,且满足∠AED=∠C,连接AD,若∠ADE=∠BAC.给出下列结论:①AD=BD;②AE=CD;③△BDE∽△ADB;④$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{1}{3}$.其中正确的结论有①②④(把所有正确结论序号都填在横线上)
如图,△ABC中,∠B=30°,∠C=45°,AB=2$\sqrt{3}$,点E在边AB上,点D在边BC上,且满足∠AED=∠C,连接AD,若∠ADE=∠BAC.给出下列结论:①AD=BD;②AE=CD;③△BDE∽△ADB;④$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{1}{3}$.其中正确的结论有①②④(把所有正确结论序号都填在横线上)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
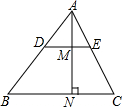 如图,△ABC,DE∥BC交AB、AC于D、E,AN⊥BC交DE于M点,若AD:DB=2:3,AM=3,则AN=$\frac{15}{2}$.若BC=8,则S△ADE=$\frac{24}{5}$.
如图,△ABC,DE∥BC交AB、AC于D、E,AN⊥BC交DE于M点,若AD:DB=2:3,AM=3,则AN=$\frac{15}{2}$.若BC=8,则S△ADE=$\frac{24}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com