
ĄūĖâÄŋĄŋČįÍžĢŽÖąÏßy=ĐxĐ4ÓëÅŨÎïÏßy=ax2+bx+cÏā―ŧÓÚAĢŽBÁ―ĩãĢŽÆäÖÐAĢŽBÁ―ĩãĩÄšáŨøąę·ÖąðΊĐ1šÍĐ4ĢŽĮŌÅŨÎïÏßđýÔĩãĢŪ
ĢĻ1ĢĐĮóÅŨÎïÏßĩÄ―âÎöĘ―Ģŧ
ĢĻ2ĢĐÔÚŨøąęÖáÉÏĘĮ·ņīæÔÚĩãCĢŽĘđĄũABCΊĩČŅüČý―ĮÐÎĢŋČôīæÔÚĢŽĮóģöĩãCĩÄŨøąęĢŽČôēŧīæÔÚĢŽĮëËĩÃũĀíÓÉĢŧ
ĢĻ3ĢĐČôĩãPĘĮÏßķÎABÉÏēŧÓëAĢŽBÖØšÏĩÄķŊĩãĢŽđýĩãPŨũPEĄÎOAĢŽÓëÅŨÎïÏßĩÚČýÏóÏÞĩÄēŋ·Ö―ŧÓÚŌŧĩãEĢŽđýĩãEŨũEGĄÍxÖáÓÚĩãGĢŽ―ŧABÓÚĩãFĢŽČôSĄũBGF=3SĄũEFP ĢŽ Įó ![]() ĩÄÖĩĢŪ
ĩÄÖĩĢŪ
Ąūīð°ļĄŋ
ĢĻ1ĢĐ
―âĢšĄßAĢŽBÁ―ĩãÔÚÖąÏßy=ĐxĐ4ÉÏĢŽĮŌšáŨøąę·ÖąðΊĐ1ĄĒĐ4ĢŽ
ĄāAĢĻĐ1ĢŽĐ3ĢĐĢŽBĢĻĐ4ĢŽ0ĢĐĢŽ
ĄßÅŨÎïÏßđýÔĩãĢŽ
Ąāc=0ĢŽ
°ŅAĄĒBÁ―ĩãŨøąęīúČëÅŨÎïÏß―âÎöĘ―ŋÉĩà ![]() ĢŽ―âĩÃ
ĢŽ―âĩÃ ![]() ĢŽ
ĢŽ
ĄāÅŨÎïÏß―âÎöĘ―ÎŠy=x2+4x
ĢĻ2ĢĐ
―âĢšĄßĄũABCΊĩČŅüČý―ĮÐÎĢŽ
ĄāÓÐAB=ACĄĒAB=BCšÍCA=CBČýÖÖĮéŋöĢŽ
ĒŲĩąAB=ACĘąĢŽĩąĩãCÔÚyÖáÉÏĢŽÉčCĢĻ0ĢŽyĢĐĢŽ
ÔōAB= ![]() =3
=3 ![]() ĢŽAC=
ĢŽAC= ![]() ĢŽ
ĢŽ
Ąā3 ![]() =
= ![]() ĢŽ―âĩÃy=Đ3Đ
ĢŽ―âĩÃy=Đ3Đ ![]() ŧōy=Đ3+
ŧōy=Đ3+ ![]() ĢŽ
ĢŽ
ĄāCĢĻ0ĢŽĐ3Đ ![]() ĢĐŧōĢĻ0ĢŽĐ3Đ
ĢĐŧōĢĻ0ĢŽĐ3Đ ![]() ĢĐĢŧ
ĢĐĢŧ
ĩąĩãCÔÚxÖáÉÏĘąĢŽÉčCĢĻxĢŽ0ĢĐĢŽÔōAC= ![]() ĢŽ
ĢŽ
Ąā ![]() =3
=3 ![]() ĢŽ―âĩÃx=Đ4ŧōx=2ĢŽĩąx=Đ4ĘąĢŽBĄĒCÖØšÏĢŽÉáČĨĢŽ
ĢŽ―âĩÃx=Đ4ŧōx=2ĢŽĩąx=Đ4ĘąĢŽBĄĒCÖØšÏĢŽÉáČĨĢŽ
ĄāCĢĻ2ĢŽ0ĢĐĢŧ
ĒÚĩąAB=BCĘąĢŽĩąĩãCÔÚxÖáÉÏĢŽÉčCĢĻxĢŽ0ĢĐĢŽ
ÔōÓÐAB=3 ![]() ĢŽBC=|x+4|ĢŽ
ĢŽBC=|x+4|ĢŽ
Ąā|x+4|=3 ![]() ĢŽ―âĩÃx=Đ4+3
ĢŽ―âĩÃx=Đ4+3 ![]() ŧōx=Đ4Đ3
ŧōx=Đ4Đ3 ![]() ĢŽ
ĢŽ
ĄāCĢĻĐ4+3 ![]() ĢŽ0ĢĐŧōĢĻĐ4Đ3
ĢŽ0ĢĐŧōĢĻĐ4Đ3 ![]() ĢŽ0ĢĐĢŧ
ĢŽ0ĢĐĢŧ
ĩąĩãCÔÚyÖáÉÏĢŽÉčCĢĻ0ĢŽyĢĐĢŽÔōBC= ![]() ĢŽ
ĢŽ
Ąā ![]() =3
=3 ![]() ĢŽ―âĩÃy=
ĢŽ―âĩÃy= ![]() ŧōy=Đ
ŧōy=Đ ![]() ĢŽ
ĢŽ
ĄāCĢĻ0ĢŽ ![]() ĢĐŧōĢĻ0ĢŽĐ
ĢĐŧōĢĻ0ĢŽĐ ![]() ĢĐĢŧ
ĢĐĢŧ
ĒÛĩąCB=CAĘąĢŽÔōĩãCÔÚÏßķÎABĩÄīđÖąÆ―·ÖÏßÓëyÖáĩÄ―ŧĩãīĶĢŽ
ĄßAĢĻĐ1ĢŽĐ3ĢĐĢŽBĢĻĐ4ĢŽ0ĢĐĢŽ
ĄāÏßķÎABĩÄÖÐĩãŨøąęΊĢĻĐ ![]() ĢŽĐ
ĢŽĐ ![]() ĢĐĢŽ
ĢĐĢŽ
ÉčÏßķÎABĩÄīđÖąÆ―·ÖÏßĩÄ―âÎöĘ―ÎŠy=x+dĢŽ
ĄāĐ ![]() =Đ
=Đ ![]() +dĢŽ―âĩÃd=1ĢŽ
+dĢŽ―âĩÃd=1ĢŽ
ĄāÏßķÎABĩÄīđÖąÆ―·ÖÏßĩÄ―âÎöĘ―ÎŠy=x+1ĢŽ
Áîx=0ŋÉĩÃy=1ĢŽÁîy=0ŋÉĮóĩÃx=Đ1ĢŽ
ĄāCĢĻĐ1ĢŽ0ĢĐŧōĢĻ0ĢŽ1ĢĐĢŧ
ŨÛÉÏŋÉÖŠīæÔÚÂúŨãĖõžþĩÄĩãCĢŽÆäŨøąęΊĢĻ0ĢŽĐ3Đ ![]() ĢĐŧōĢĻ0ĢŽĐ3Đ
ĢĐŧōĢĻ0ĢŽĐ3Đ ![]() ĢĐŧōĢĻĐ4+3
ĢĐŧōĢĻĐ4+3 ![]() ĢŽ0ĢĐŧōĢĻĐ4Đ3
ĢŽ0ĢĐŧōĢĻĐ4Đ3 ![]() ĢŽ0ĢĐŧōĢĻĐ1ĢŽ0ĢĐŧōĢĻ0ĢŽ1ĢĐŧōĢĻ2ĢŽ0ĢĐŧōĢĻ0ĢŽ
ĢŽ0ĢĐŧōĢĻĐ1ĢŽ0ĢĐŧōĢĻ0ĢŽ1ĢĐŧōĢĻ2ĢŽ0ĢĐŧōĢĻ0ĢŽ ![]() ĢĐŧōĢĻ0ĢŽĐ
ĢĐŧōĢĻ0ĢŽĐ ![]() ĢĐ
ĢĐ
ĢĻ3ĢĐ
―âĢšđýĩãPŨũPQĄÍEFĢŽ―ŧEFÓÚĩãQĢŽđýĩãAŨũADĄÍxÖáÓÚĩãDĢŽ
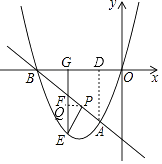
ĄßPEĄÎOAĢŽGEĄÎADĢŽ
ĄāĄÏOAD=ĄÏPEGĢŽĄÏPQE=ĄÏODA=90ĄãĢŽ
ĄāĄũPQEĄŨĄũODAĢŽ
Ąā ![]() =3ĢŽžīEQ=3PQĢŽ
=3ĢŽžīEQ=3PQĢŽ
ĄßÖąÏßABĩÄ―âÎöĘ―ÎŠy=ĐxĐ4ĢŽ
ĄāĄÏABO=45Ąã=ĄÏPFQĢŽ
ĄāPQ=FQĢŽBG=GFĢŽ
ĄāEF=4PQĢŽ
ĄāGE=GF+4PQĢŽ
ĄßSĄũBGF=3SĄũEFPĢŽ
Ąā ![]() GF2=3ĄÁ
GF2=3ĄÁ ![]() 4PQ2ĢŽ
4PQ2ĢŽ
ĄāGF=2 ![]() PQĢŽ
PQĢŽ
Ąā ![]() =
= ![]() =
= ![]()
Ąū―âÎöĄŋĢĻ1ĢĐÓÉÖąÏß―âÎöĘ―ŋÉ·ÖąðĮóĩÃAĄĒBÁ―ĩãĩÄŨøąęĢŽĀûÓÃīýķĻÏĩĘý·ĻŋÉĮóĩÃÅŨÎïÏß―âÎöĘ―ĢŧĢĻ2ĢĐĩąAB=ACĘąĢŽĩãCÔÚyÖáÉÏĢŽŋÉąíĘūģöACĩÄģĪķČĢŽŋÉĮóĩÃÆäŨøąęĢŧĩąAB=BCĘąĢŽŋÉÖŠĩãCÔÚxÖáÉÏĢŽŋÉąíĘūģöBCĩÄģĪķČĢŽŋÉĮóĩÃÆäŨøąęĢŧĩąAC=BCĘąĩãCÔÚÏßķÎABĩÄīđÖąÆ―·ÖÏßÓëŨøąęÖáĩÄ―ŧĩãīĶĢŽŋÉĮóĩÃÏßķÎABĩÄÖÐĩãĩÄŨøąęĢŽŋÉĮóĩÃīđÖąÆ―·ÖÏßĩÄ―âÎöĘ―ĢŽÔōŋÉĮóĩÃCĩãŨøąęĢŧĢĻ3ĢĐđýĩãPŨũPQĄÍEFĢŽ―ŧEFÓÚĩãQĢŽđýĩãAŨũADĄÍxÖáÓÚĩãDĢŽŋÉÖĪÃũĄũPQEĄŨĄũODAĢŽŋÉĮóĩÃEQ=3PQĢŽÔŲ―ášÏFĩãÔÚÖąÏßABÉÏĢŽŋÉĮóĩÃFQ=PQĢŽÔōŋÉĮóĩÃEF=4PQĢŽĀûÓÃČý―ĮÐÎĩÄÃæŧýĩÄđØÏĩŋÉĮóĩÃGFÓëPQĩÄđØÏĩĢŽÔōŋÉĮóĩÃąČÖĩĢŪ


 ÃûÐĢŋÎĖÃÏĩÁÐīð°ļ
ÃûÐĢŋÎĖÃÏĩÁÐīð°ļ
| Äęžķ | ļßÖÐŋÎģĖ | Äęžķ | ģõÖÐŋÎģĖ |
| ļßŌŧ | ļßŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõŌŧ | ģõŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßķþ | ļßķþÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõķþ | ģõķþÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßČý | ļßČýÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõČý | ģõČýÃâ·ŅŋÎģĖÍÆžöĢĄ |
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋÕÛĩþČý―ĮÐÎÖ―ÆŽABCĢŽĘđĩãAÂäÔÚBCąßÉÏĩÄĩãFĢŽĮŌÕÛšÛDEĄÎBCĢŽČôĄÏA=75ĄãĢŽĄÏC=60ĄãĢŽÔōĄÏBDF=____________________________

ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽÔÚRtĄũABCÖÐĢŽĄÏB=90ĄãĢŽBC=5 ![]() ĢŽĄÏC=30ĄãĢŪĩãDīÓĩãCģö·ĒŅØCA·―ÏōŌÔÃŋÃë2ļöĩĨÎŧģĪĩÄËŲķČÏōĩãAÔČËŲÔËķŊĢŽÍŽĘąĩãEīÓĩãAģö·ĒŅØAB·―ÏōŌÔÃŋÃë1ļöĩĨÎŧģĪĩÄËŲķČÏōĩãBÔČËŲÔËķŊĢŽĩąÆäÖÐŌŧļöĩãĩ―īïÖÕĩãĘąĢŽÁíŌŧļöĩãŌēËæÖŪÍĢÖđÔËķŊĢŪÉčĩãDĄĒEÔËķŊĩÄĘąžäĘĮtÃëĢĻtĢū0ĢĐĢŪđýĩãDŨũDFĄÍBCÓÚĩãFĢŽÁŽ―ÓDEĄĒEFĢŪ
ĢŽĄÏC=30ĄãĢŪĩãDīÓĩãCģö·ĒŅØCA·―ÏōŌÔÃŋÃë2ļöĩĨÎŧģĪĩÄËŲķČÏōĩãAÔČËŲÔËķŊĢŽÍŽĘąĩãEīÓĩãAģö·ĒŅØAB·―ÏōŌÔÃŋÃë1ļöĩĨÎŧģĪĩÄËŲķČÏōĩãBÔČËŲÔËķŊĢŽĩąÆäÖÐŌŧļöĩãĩ―īïÖÕĩãĘąĢŽÁíŌŧļöĩãŌēËæÖŪÍĢÖđÔËķŊĢŪÉčĩãDĄĒEÔËķŊĩÄĘąžäĘĮtÃëĢĻtĢū0ĢĐĢŪđýĩãDŨũDFĄÍBCÓÚĩãFĢŽÁŽ―ÓDEĄĒEFĢŪ 
ĢĻ1ĢĐĮóÖĪĢšAE=DFĢŧ
ĢĻ2ĢĐËÄąßÐÎAEFDÄÜđŧģÉΊÁâÐÎÂðĢŋČįđûÄÜĢŽĮóģöÏāÓĶĩÄtÖĩĢŧČįđûēŧÄÜĢŽËĩÃũĀíÓÉĢŪ
ĢĻ3ĢĐĩątΊšÎÖĩĘąĢŽĄũDEFΊֹ―ĮČý―ĮÐÎĢŋĮëËĩÃũĀíÓÉĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠĢšËÄąßÐÎABCDĩÄķÔ―ĮÏßACĄĒBDÏā―ŧÓÚĩãOĢŽÔōÏÂÁÐĖõžþēŧÄÜÅÐķĻËÄąßÐÎABCDĘĮÆ―ÐÐËÄąßÐÎĩÄĘĮ![]() ĄĄĄĄ
ĄĄĄĄ![]()
A. ![]() ĢŽ
ĢŽ![]() B.
B. ![]() ĢŽ
ĢŽ![]()
C. ![]() ĢŽ
ĢŽ![]() D.
D. ![]() ĢŽ
ĢŽ![]()
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽŌŅÖŠÖąÏßABĢŽCDÏā―ŧÓÚĩãOĢŽOEÆ―·ÖĄÏAODĢŽFOĄÍABĢŽīđŨãΊOĢŽ![]() ĄÏBOD=ĄÏDOEĢŪ
ĄÏBOD=ĄÏDOEĢŪ
ĢĻ1ĢĐĮóĄÏBOFĩÄķČĘýĢŧ
ĢĻ2ĢĐĮëÐīģöÍžÖÐÓëĄÏBODÏāĩČĩÄËųÓÐĩÄ―ĮĢŪ

ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋÔÚÆ―ÃæÄÚ,·ÖąðÓÃ3ļųĄĒ5ļųĄĒ6ļųĄĄŧðēņ°ôĘŨÎēŌĀīÎÏā―Ó,ÄÜīîģÉĘēÃīÐÎŨīĩÄČý―ĮÐÎÄØ?ÍĻđýģĒĘÔ,ÁÐąíČįÏÂ.
ŧðēņ°ôĘý | 3 | 5 | 6 | Ą |
ĘūŌâÍž |
|
|
| Ą |
ÐÎŨī | ĩČąßČý―ĮÐÎ | ĩČŅüČý―ĮÐÎ | ĩČąßČý―ĮÐÎ | Ą |
ÎĘ:(1)4ļųŧðēņ°ôÄÜīîģÉČý―ĮÐÎÂð?
(2)8ļųĄĒ12ļųŧðēņ°ô·ÖąðÄÜīîģÉžļÖÖēŧÍŽÐÎŨīĩÄČý―ĮÐÎ?ēĒŧģöËüÃĮĩÄĘūŌâÍž.
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽÔÚÉČÐÎOABÖÐĢŽĄÏO=60ĄãĢŽOA=4 ![]() ĢŽËÄąßÐÎOECFĘĮÉČÐÎOABÖÐŨîīóĩÄÁâÐÎĢŽÆäÖÐĩãEĢŽCĢŽF·ÖąðÔÚOAĢŽ
ĢŽËÄąßÐÎOECFĘĮÉČÐÎOABÖÐŨîīóĩÄÁâÐÎĢŽÆäÖÐĩãEĢŽCĢŽF·ÖąðÔÚOAĢŽ ![]() ĢŽOBÉÏĢŽÔōÍžÖÐŌõÓ°ēŋ·ÖĩÄÃæŧýΊ ĢŪ
ĢŽOBÉÏĢŽÔōÍžÖÐŌõÓ°ēŋ·ÖĩÄÃæŧýΊ ĢŪ 
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋ―âÏÂÁз―ģĖĢš
ĢĻ1ĢĐx+2ĢĻ5Đ3xĢĐ=15Đ3ĢĻ7Đ5xĢĐ
ĢĻ2ĢĐ![]()
ĢĻ3ĢĐ![]()
ĢĻ4ĢĐ![]() ĢŪ
ĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋÏÖÓÐÕý·―ÐÎABCDšÍŌŧļöŌÔOΊֹ―ĮķĨĩãĩÄČý―Į°åĢŽŌÆķŊČý―Į°åĢŽĘđČý―Į°åĩÄÁ―Öą―ĮąßËųÔÚÖąÏß·ÖąðÓëÖąÏßBCĢŽCD―ŧÓÚĩãMĢŽNĢŪ
ĢĻ1ĢĐČįÍž1ĢŽČôĩãOÓëĩãAÖØšÏĢŽÔōOMÓëONĩÄĘýÁŋđØÏĩĘĮ__________________Ģŧ
ĢĻ2ĢĐČįÍž2ĢŽČôĩãOÔÚÕý·―ÐÎĩÄÖÐÐÄĢĻžīÁ―ķÔ―ĮÏßĩÄ―ŧĩãĢĐĢŽÔōĢĻ1ĢĐÖÐĩÄ―áÂÛĘĮ·ņČÔČŧģÉÁĒĢŋĮëËĩÃũĀíÓÉĢŧ
ĢĻ3ĢĐČįÍž3ĢŽČôĩãOÔÚÕý·―ÐÎĩÄÄÚēŋĢĻšŽąß―įĢĐĢŽĩąOM=ONĘąĢŽĮëĖ―ūŋĩãOÔÚŌÆķŊđýģĖÖÐŋÉÐÎģÉĘēÃīÍžÐÎĢŋ
ĢĻ4ĢĐČįÍž4ĘĮĩãOÔÚÕý·―ÐÎÍâēŋĩÄŌŧÖÖĮéŋöĢŪĩąOM=ONĘąĢŽĮëÄãūÍĄ°ĩãOĩÄÎŧÖÃÔÚļũÖÖĮéŋöÏÂĢĻšŽÍâēŋĢĐŌÆķŊËųÐÎģÉĩÄÍžÐÎĄąĖáģöŌŧļöÕýČ·ĩÄ―áÂÛĢŪĢĻēŧąØËĩĀíĢĐ

ēéŋīīð°ļšÍ―âÎö>>
°ŲķČÖÂÐÅ - Á·Ï°ēáÁÐąí - ĘÔĖâÁÐąí
šþąąĘĄŧĨÁŠÍøÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻÆ―ĖĻ | ÍøÉÏÓКĶÐÅÏĒūŲąĻŨĻĮø | ĩįÐÅÕĐÆūŲąĻŨĻĮø | ÉæĀúĘ·ÐéÎÞÖũŌåÓКĶÐÅÏĒūŲąĻŨĻĮø | ÉæÆóĮÖČĻūŲąĻŨĻĮø
ÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻĩįŧ°Ģš027-86699610 ūŲąĻÓĘÏäĢš58377363@163.com