
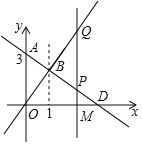
【题目】如图,A点的纵坐标为3,过A点的一次函数图象与正比例函数y=2x的图象相交于点B.
(1)求该一次函数的表达式;
(2)若点P为第一象限内直线AB上的一动点,设点P的横坐标为m,过点P作x轴的垂线交正比例函数图象于点Q,交x轴于点M.
①当△AOB≌△PQB时,求线段PM的长.
②当线段PQ=![]() AO时,请直接写出点P的坐标.
AO时,请直接写出点P的坐标.
【答案】(1)y=﹣x+3;(2)①1;②点P的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)根据图象上点的坐标特征求得B的坐标,然后根据待定系数法即可求得一次函数的解析式;
(2)①根据题意P(m,﹣m+3),则Q(m,2m),即可得到PQ=|2m﹣(﹣m+3)|=|3m﹣3|,当△AOB≌△PQB时,AO=PQ,即|3m﹣3|=3,然后结合题意即可求得P(2,1),PM=1;
②根据题意得到|3m﹣3|=![]() ,求得m的值,从而求得P的坐标.
,求得m的值,从而求得P的坐标.
解:(1)∵点B的横坐标为1,且点B在正比例函数y=2x的图象上,
∴y=2×1=2,
∴B(1,2),
∵A点的纵坐标为3,
设一次函数的解析式为y=kx+3,
代入B(1,2)得,2=k+3,
解得k=﹣1,
∴一次函数的解析式为y=﹣x+3;
(2)①∵点P为第一象限内直线AB上的一动点,且点P的横坐标为m,
∴P(m,﹣m+3),
∵PQ⊥x轴,且Q在y=2x的图象上,
∴Q(m,2m),
∴PQ=|2m﹣(﹣m+3)|=|3m﹣3|,
当△AOB≌△PQB时,
∴AO=PQ,即|3m﹣3|=3,
∴m=2或0(由点P在第一象限,故舍去),
∴P(2,1),PM=1;
②当线段PQ=![]() AO时,则|3m﹣3|=
AO时,则|3m﹣3|=![]() ,
,
当3m﹣3=![]() 时,
时,
解得m=![]() ,
,
此时P(![]() ,
,![]() );
);
当﹣3m+3=![]() 时,
时,
解得m=![]() ,
,
此时P(![]() ,
,![]() ).
).
综上:点P的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠ABC=90°,AB=3,BC=4,过点B的直线把△ABC分割成两个三角形,使其中只有一个是等腰三角形,则这个等腰三角形的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面三行数:
-2、4、-8、16、-32、64、……①
0、6、-6、18、-30、66、……②
-1、2、-4、8、-16、32、……③
设x、y、z分别为第①②③行的第10个数,则2x-y-2z的值为( )
A. ![]() B. 0C. -2D. 2
B. 0C. -2D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为及时救治新冠肺炎重症患者,某医院需购买A、B两种型号的呼吸机.已知购买一台A型呼吸机需6万元,购买一台B型呼吸机需4万元,该医院准备投入资金y万元,全部用于购进35台这两种型号的呼吸机,设购进A型呼吸机x台.
(1)求y关于x的函数关系式;
(2)若购进B型呼吸机的数量不超过A型呼吸机数量的2倍,则该医院至少需要投入资金多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
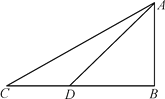
【题目】如图,某校数学兴趣小组为测得校园里旗杆AB的高度,在操场的平地上选择一点C,测得旗杆顶端A的仰角为30,再向旗杆的方向前进16米,到达点D处(C,D,B三点在同一直线上),又测得旗杆顶端A的仰角为45,请计算旗杆AB的高度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设二次函数y1,y2的图象的顶点分别为(a,b)、(c,d),当a=﹣c,b=2d,且开口方向相同时,则称y1是y2的“反倍顶二次函数”.
(1)请写出二次函数y=x2+x+1的一个“反倍顶二次函数”;
(2)已知关于x的二次函数y1=x2+nx和二次函数y2=nx2+x,函数y1+y2恰是y1﹣y2的“反倍顶二次函数”,求n.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 若AP=BP,则点P是线段的中点 B. 若点C在线段AB上,则AB=AC+BC
C. 若AC+BC>AB,则点C一定在线段AB外 D. 两点之间,线段最短
查看答案和解析>>
科目:初中数学 来源: 题型:
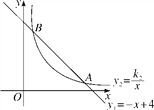
【题目】如图,函数y1=-x+4的图象与函数y2=![]() (x>0)的图象交于A(a,1)、B(1,b)两点.
(x>0)的图象交于A(a,1)、B(1,b)两点.
(1)求函数y2的表达式;
(2)观察图象,比较当x>0时,y1与y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是反比例函数![]() 的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为______.
的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com