

分析 (1)延长FD到点G.使DG=BE.连结AG,即可证明△ABE≌△ADG,可得AE=AG,再证明△AEF≌△AGF,可得EF=FG,即可解题;
(2)延长FD到点G.使DG=BE.连结AG,即可证明△ABE≌△ADG,可得AE=AG,再证明△AEF≌△AGF,可得EF=FG,即可解题;
(3)连接EF,延长AE、BF相交于点C,然后与(2)同理可证.
解答 解:(1)EF=BE+DF,证明如下:
在△ABE和△ADG中,
$\left\{\begin{array}{l}{DG=BE}\\{∠B=∠ADG}\\{AB=AD}\end{array}\right.$,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=$\frac{1}{2}$∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
$\left\{\begin{array}{l}{AE=AG}\\{∠EAF=∠GAF}\\{AF=AF}\end{array}\right.$,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
故答案为 EF=BE+DF.
(2)结论EF=BE+DF仍然成立;
理由:延长FD到点G.使DG=BE.连结AG,如图2,
在△ABE和△ADG中,$\left\{\begin{array}{l}{DG=BE}\\{∠B=∠ADG}\\{AB=AD}\end{array}\right.$,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=$\frac{1}{2}$∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
$\left\{\begin{array}{l}{AE=AG}\\{∠EAF=∠GAF}\\{AF=AF}\end{array}\right.$,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
(3)如图3,连接EF,延长AE、BF相交于点C,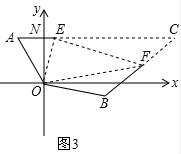
∵∠AOB=30°+90°+(90°-70°)=140°,∠EOF=70°,
∴∠EOF=$\frac{1}{2}$∠AOB,
又∵OA=OB,∠OAC+∠OBC=(90°-30°)+(70°+50°)=180°,
∴符合探索延伸中的条件,
∴结论EF=AE+BF成立,
即EF=2×(45+60)=210(海里).
答:此时两舰艇之间的距离是210海里.
点评 本题考查了全等三角形的判定以及全等三角形对应边相等的性质,本题中求证△AEF≌△AGF是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1),(2,1).
如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1),(2,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
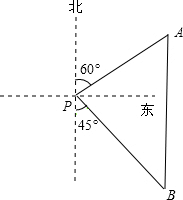 如图,一艘海轮位于灯塔P的北偏东60°方向,距灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,此时B处距离灯塔P有多远(结果取整数).参考数值:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4.
如图,一艘海轮位于灯塔P的北偏东60°方向,距灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,此时B处距离灯塔P有多远(结果取整数).参考数值:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
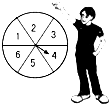 如图所示,转盘被等分成六个扇形,并在上面一次写上数字1、2、3、4、5、6;若自由转动转盘,当它停止转动时,求:
如图所示,转盘被等分成六个扇形,并在上面一次写上数字1、2、3、4、5、6;若自由转动转盘,当它停止转动时,求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 多面体 | 各面形状 | 面数(F) | 顶点数(V) | 棱数(E) |
| 四面体 | 三角形 | 4 | 4 | 6 |
| 长方体 | 长方形 | 6 | 8 | x |
| 正八面体 | 正三角形 | 8 | y | 12 |
| 正十二面体 | 正五面型 | 12 | 20 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 赚24元 | B. | 赔24元 | C. | 不赚不赔 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校七年级(一)班共有50名学生,分别参加了写作、数学、英语、篮球及摄影兴趣小组,每个学生必须参加且只能参加其中一种,请根据如图所示的扇形统计图.求:
某校七年级(一)班共有50名学生,分别参加了写作、数学、英语、篮球及摄影兴趣小组,每个学生必须参加且只能参加其中一种,请根据如图所示的扇形统计图.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com