
【题目】如图,已知PA、PB切⊙O于A,B两点,连AB,且PA,PB的长是方程x2﹣2mx+3=0的两根,AB=m.试求: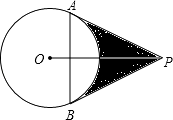
(1)⊙O的半径;
(2)由PA,PB, ![]() 围成图形(即阴影部分)的面积.
围成图形(即阴影部分)的面积.
【答案】
(1)解:连OA,OB,

∵PA=PB,
∴△=(﹣2m)2﹣4×3=0,
∴m2=3,m>0,
∴m= ![]() ,
,
∴x2﹣2 ![]() x+3=0,
x+3=0,
∴x1=x2= ![]() ,
,
∴PA=PB=AB= ![]() ,
,
∴△ABP等边三角形,
∴∠APB=60°,
∴∠APO=30°,
∵PA= ![]() ,
,
∴OA=1
(2)解:∵∠AOP=60°,
∴∠AOB=120°,
S阴=S四边形OAPB﹣S扇形OAB
=2S△AOP﹣S扇形OAB
=2× ![]() ×1×
×1× ![]() ﹣
﹣ ![]() ,
,
= ![]() ﹣
﹣ ![]() π.
π.
【解析】(1)由已知易证PA=PA,而PA、PB是一元二次方程的两个根,可知一元二次方程由两个相等的实数根,根据b2-4ac=0,建立方程,即可求出m的值,再证明△ABP等边三角形,就可求出圆的半径长。
(2)观察图形S阴=2S△AOP﹣S扇形OAB,分别求出△AOP和扇形OAB的面积即可。
【考点精析】掌握公式法和求根公式是解答本题的根本,需要知道要用公式解方程,首先化成一般式.调整系数随其后,使其成为最简比.确定参数abc,计算方程判别式.判别式值与零比,有无实根便得知.有实根可套公式,没有实根要告之;根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根.


科目:初中数学 来源: 题型:
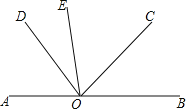
【题目】如图,已知,A、O、B在同一条直线上,∠AOE=∠COD,∠EOD=30°.
(1)若∠AOE=88°30′,求∠BOC的度数;
(2)若射线OC平分∠EOB,求∠BOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,D,E是边AB上两点,且CE所在直线垂直平分线段AD,CD平分∠BCE,AC=5cm,则BD的长为( )
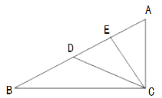
A. 5cm B. 6cm C. 7cm D. 8cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三个生产日光灯管的厂家在广告中宣称,他们生产的日光灯管在正常情况下,灯管的使用寿命为12个月.工商部门为了检查他们宣传的真实性,从三个厂家各抽取11只日光灯管进行检测,灯管的使用寿命(单位:月)如下:

(1)这三个厂家的广告,分别利用了统计中的哪一个特征数(平均数、中位数、众数)进行宣传?
(2)如果三个厂家产品的售价一样,作为顾客的你选购哪个厂家的产品?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上的一点,且AD∥CO. 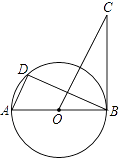
(1)求证:△ABD≌△OBC;
(2)若AB=2,BC= ![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC 的顶点分别为 A(-2,2)、B(-4,5)、C(-5,1)和直线 m (直线 m 上各点的 横坐标都为 1).
(1)作出△ABC 关于 x 轴对称的图形△A1B1C1,并写出点 B1 的坐标;
(2)作出△ABC 关于 y 轴对称的图形△A2 B2C2,并写出点 B2 的坐标;
(3)若点 P( a,b )是△ABC 内部一点,写出点 P 关于直线 m 对称的点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
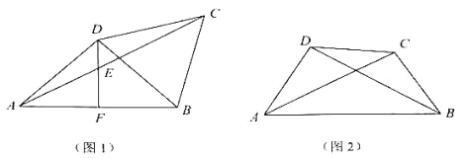
【题目】在四边形 ABCD 中,BC=CD,连接 AC、BD,∠ADB=90°.
(1)如图 1,若 AD=BD=BC,过点 D 作 DF⊥AB 于点 F,交 AC 于点 E:
①求∠DAC;
②猜想 AE、DE、CE 的数量关系,并证明你的猜想;
(2)如图 2,若 AC=BD,求∠DAC 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x=﹣3是关于x的方程(k+3)x+2=3x﹣2k的解.
(1)求k的值;
(2)在(1)的条件下,已知线段AB=6cm,点C是直线AB上一点,且BC=kAC,若点D是AC的中点,求线段CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com