
����Ŀ����ͼ1����ABC�ǵ���ֱ�������Σ���BAC�� 90����AB��AC���ı���ADEF�������Σ���B��C�ֱ��ڱ�AD��AF�ϣ���ʱBD��CF��BD��CF������

��1������ABC�Ƶ�A��ʱ����ת����0��������90����ʱ����ͼ2��BD��CF����������������֤����������������˵�����ɣ�
��2������ABC�Ƶ�A��ʱ����ת45��ʱ����ͼ3���ӳ�DB��CF�ڵ�H.
����֤��BD��CF��
����AB��2��AD��3![]() ʱ�����߶�DH�ij���
ʱ�����߶�DH�ij���
���𰸡���1��BD��CF���������������������2���������������![]() .
.
��������
�����������1��������SAS��֤����CAF�ա�BAD,����ȫ�������ε����ʼ��ɵ�BD��CF��������2��������HFN����AND���ڽǺ��Լ����ǵĵȽǣ��õ���NHF��90��,���ɵ����Ľ��ۣ���3������DF���ӳ�AB����DF���ڵ�M��������BMD�ס�FHD���.
�����������l���⣺BD��CF������
֤������AC��AB����CAF����BAD����;AF��AD,��ABD�ա�ACF,��BD��CF.
��2����֤��������1���ã���ABD�ա�ACF�����HFN����ADN��
����HFN����ADN�У��ߡ�HFN����AND����HNF����AND,���NHF����NAD��90��,
��HD��HF,��BD��CF.
���⣺��ͼ������DF���ӳ�AB����DF���ڵ�M.
����MAD�У��ߡ�MAD����MDA��45�������BMD��90��.
��Rt��BMD��Rt��FHD�У��ߡ�MDB����HDF,���BMD�ס�FHD.
��AB��2��AD��3![]() ���ı���ADEF�������Σ���MA��MD��
���ı���ADEF�������Σ���MA��MD��![]() ��3.
��3.
��MB��3��2��1,DB��![]() ��
��![]() .
.
��![]() ��
��![]() .��
.��![]() ��
��![]() .
.
��DH��![]() .
.




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
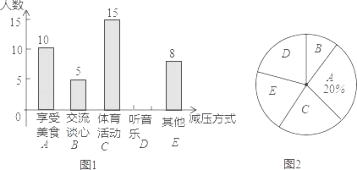
����Ŀ����ͼ��AC�ǡ�O��ֱ����AB�ǡ�O���ң���E�ǻ�AB���е㣬����OE����AB�ڵ�D��������CD����tan��CDB=![]() ,��AB��DE��������ϵ�ǣ� ��
,��AB��DE��������ϵ�ǣ� ��
A. AB=2DE B. AB=3DE C. AB=4DE D. 2AB=3DE
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ĵ����(��2��6)���ӳɵ��߶��У���x���y�ᶼ���ཻ����( )
A. (��4��2) B. (3����1) C. (4��2) D. (��3����1)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
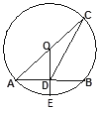
����Ŀ��ijУ������1���ಿ��ͬѧ����һ������Ϊ�����ʺ��Լ��Ŀ�ǰ��ѹ��ʽ���ĵ������ռ��������ݺ���ʦ����ѹ��ʽ��Ϊ���࣬��������ͼ1��ͼ2������������ͳ��ͼ�������ͼ�е���Ϣ����������⣮
��1��������1������ܵ����ͬѧ���ж�������
��2����ȫ����ͳ��ͼ������գ������ֵ� �ˣ�����ͳ��ͼ�С������C������Ӧ��Բ�ĽǶ��� ��
��3����ϲ��������̸�ġ���5��ͬѧ������������������Ů������ʦ���5��ͬѧ����ѡ����ͬѧ���н���������״ͼ���б�����ѡȡ������ͬѧ����Ů���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʒԭ��ÿ���ɱ�128Ԫ�������������꼼��������ǿ��������ÿ���ɱ���Ϊ98Ԫ������ɱ�ÿ���½��İٷ�����ͬ����ÿ���ƽ���½���Ϊx������з���Ϊ�� ��
A. 128(1��x)2 = 98B. 128(1+x)2= 98
C. 98(1��x)2 = 128D. 98(1+x)2 = 128
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ⷽ��
��1��|��3|+�� ![]() ��1��0��
��1��0�� ![]() +��
+�� ![]() ����1��
����1��
��2���ⷽ���� 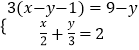 ��
��
��3����x��ֵ��25��x+2��2��36=0��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com