
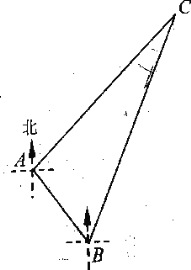
【题目】“雪龙”号考察船在某海域进行科考活动,在点 A 处测得小岛C 在它的东北方向上,它沿南偏东37°方向航行 2 海里到达点 B 处,又测得小岛C 在它的北偏东23°方向上(如图所示),求“雪龙”号考察船在点 B 处与小岛C 之间的距离.(参考数据: sin22°0.37 , cos22°0.93 , tan 22° 0.40 ,![]() 1.4 ,
1.4 ,![]() 1.7 )
1.7 )
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为建设最美恩施,一旅游投资公司拟定在某景区用茶花和月季打造一片人工花海,经市场调查,购买![]() 株茶花与
株茶花与![]() 株月季的费用相同,购买
株月季的费用相同,购买![]() 株茶花与
株茶花与![]() 株月季共需
株月季共需![]() 元.
元.
(1)求茶花和月季的销售单价;
(2)该景区至少需要茶花月季共![]() 株,要求茶花比月季多
株,要求茶花比月季多![]() 株,但订购两种花的总费用不超过
株,但订购两种花的总费用不超过![]() 元,该旅游投资公司怎样购买所需总费用最低,最低费用是多少.
元,该旅游投资公司怎样购买所需总费用最低,最低费用是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
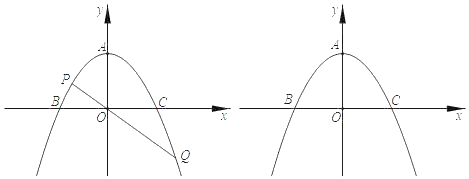
【题目】已知:如图,抛物线![]() 的顶点为A(0,2),与x轴交于B(﹣2,0)、C(2,0)两点.
的顶点为A(0,2),与x轴交于B(﹣2,0)、C(2,0)两点.
(1)求抛物线![]() 的函数表达式;
的函数表达式;
(2)设点P是抛物线y上的一个动点,连接PO并延长至点Q,使OQ=2OP.若点Q正好落在该抛物线上,求点P的坐标;
(3)设点P是抛物线y上的一个动点,连接PO并延长至点Q,使OQ=mOP(m为常数);
①证明点Q一定落在抛物线![]() 上;
上;
②设有一个边长为m+1的正方形(其中m>3),它的一组对边垂直于x轴,另一组对边垂直于y轴,并且该正方形四个顶点正好落在抛物线![]() 和
和![]() 组成的封闭图形上,求线段PQ被该正方形的两条边截得线段长最大时点Q的坐标.
组成的封闭图形上,求线段PQ被该正方形的两条边截得线段长最大时点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]() 的值是_______.
的值是_______.
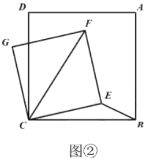
(2)如图②,在正方形![]() 中,
中,![]() ,点
,点![]() 是平面上一动点,且
是平面上一动点,且![]() ,连接
,连接![]() ,在
,在![]() 上方作正方形
上方作正方形![]() ,求线段
,求线段![]() 的最大值.
的最大值.
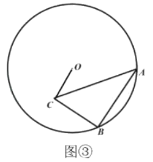
问题解决:(3)如图③,![]() 半径为6,在
半径为6,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 内,且
内,且![]() .当点
.当点![]() 在圆上运动时,求线段
在圆上运动时,求线段![]() 的最小值.
的最小值.
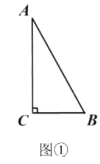
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在矩形ABCD中,对角线AC与BD相交于点O,过点C作BD的平行线,过点D作AC的平行线,两线交于点P.
①求证:四边形CODP是菱形.
②若AD=6,AC=10,求四边形CODP的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB为直径, OD∥BC交⊙O于点D,交AC于点E,连接AD,BD,CD.
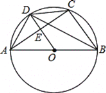
(1)求证:AD=CD;
(2)若AB=10,cos∠ABC=![]() ,求tan∠DBC的值.
,求tan∠DBC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
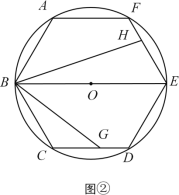
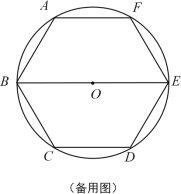
【题目】如图,已知圆O是正六边形ABCDEF外接圆,直径BE=8,点G、H分别在射线CD、EF上(点G不与点C、D重合),且∠GBH=60°,设CG=x,EH=y.
(1)如图①,当直线BG经过弧CD的中点Q时,求∠CBG的度数;
(2)如图②,当点G在边CD上时,试写出y关于x的函数关系式,并写出x的取值范围;
(3)联结AH、EG,如果△AFH与△DEG相似,求CG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
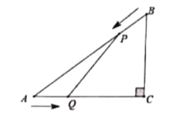
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 由点
由点![]() 出发沿
出发沿![]() 方向向点
方向向点![]() 匀速运动,同时点
匀速运动,同时点![]() 由点
由点![]() 出发沿
出发沿![]() 方向向点
方向向点![]() 匀速运动,它们的速度均为
匀速运动,它们的速度均为![]() .连接
.连接![]() ,设运动时间为
,设运动时间为![]() .
.
(1)当![]() 为何值时,
为何值时,![]() ?
?
(2)设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并求出当
的函数关系式,并求出当![]() 为何值时,
为何值时,![]() 取得最大值?
取得最大值?![]() 的最大值是多少?
的最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com