
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,D是AC边上一动点,CE⊥BD于E.

(1)如图(1),若BD平分∠ABC时,①求∠ECD的度数;②延长CE交BA的延长线于点F,补全图形,探究BD与EC的数量关系,并证明你的结论;
(2)如图(2),过点A作AF⊥BE于点F,猜想线段BE,CE,AF之间的数量关系,并证明你的猜想.
【答案】(1)①22.5°②BD=2CE(2)BE﹣CE=2AF
【解析】试题分析:(1)①根据等腰直角三角形的性质得出∠CBA=45°,再利用角平分线的定义解答即可;②延长CE交BA的延长线于点F得出CE=FE,再利用AAS证明△ABD≌△ACF,利用全等三角形的性质解答即可;(2)过点A作AH⊥AE,交BE于点H,证明△ABH≌△ACE,进而得出CE=BH,利用等腰直角三角形的判定和性质解答即可.
试题解析:
(1)①∵在△ABC中,∠BAC=90°,AB=AC,
∴∠CBA=45°,∵BD平分∠ABC,∴∠DBA=22.5°,
∵CE⊥BD,∴∠ECD+∠CDE=90°,∠DBA+∠BDA=90°,
∵∠CDE=∠BDA,∴∠ECD=∠DBA=22.5°;
②BD=2CE.
证明:延长CE交BA的延长线于点F,如图1,
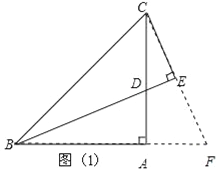
∵BD平分∠ABC,CE⊥BD,
∴CE=FE,
在△ABD与△ACF中,
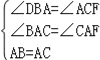 ,
,
∴△ABD≌△ACF(AAS),
∴BD=CF=2CE;
(2)结论:BE﹣CE=2AF.
证明:过点A作AH⊥AE,交BE于点H,如图2,

∵AH⊥AE,
∴∠BAH+∠HAC=∠HAC+∠CAE,
∴∠BAH=∠CAE,
在△ABH与△ACE中,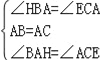 ,
,
∴△ABH≌△ACE(ASA),
∴CE=BH,AH=AE,
∴△AEH是等腰直角三角形,
∴AF=EF=HF,
∴BE﹣CE=2AF.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】下列从左到右的运算是因式分解的是( )
A. 2a2﹣2a+1=2a(a﹣1)+1 B. (x﹣y)(x+y)=x2﹣y2
C. 9x2﹣6x+1=(3x﹣1)2 D. x2+y2=(x﹣y)2+2xy
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=110°,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.

(1)求∠DAF的度数;
(2)如果BC=10cm,求△DAF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成证明并写出推理根据: 已知,如图,∠1=132°,∠ACB=48°,∠2=∠3,FH⊥AB于H.
求证:CD⊥AB.
证明:∵∠1=132°,∠ACB=48°,
∴∠1+∠ACB=180°
∴DE∥BC
∴∠2=()
又∵∠2=∠3
∴∠3=∠DCB
∴HF∥()
∴∠CDB= . ()
又∵FH⊥AB,
∴∠FHB=()
∴∠CDB=°.
∴CD⊥AB.()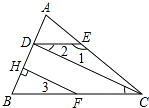
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com