练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
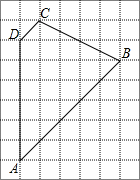
    10．如图所示，图中小正方形的边长为1，试求图中梯形ABCD的面积，你有哪些方法？与同伴进行交流．

    分析 方法一：根据四边形所在的矩形的面积减去四周三个直角三角形的面积列式计算即可得解；
    方法二：根据网格结构，把四边形分成一个梯形和二个三角形，然后列式计算即可得解．

    解答 解：方法一：四边形ABCD的面积=7×5-$\frac{1}{2}$×5×5-$\frac{1}{2}$×2×4-$\frac{1}{2}$×1×1，
    =35-17，
    =18；
    方法二：四边形ABCD的面积=$\frac{1}{2}$×5×5+$\frac{1}{2}$×3×1+$\frac{（3+5）×1}{2}$，
    =18．

    点评 本题考查了三角形的面积，对于不规则图形的面积的求解，把不规则转化为用规则图形的面积表示是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    3．一个正方体的体积变为原来的0.001倍，它的棱长是原来的多少倍？体积变为原来的1000倍呢？体积变为原来的1000000倍呢？利用你发现的规律解决下列问题：
    若$\root{3}{0.00000526}$=0.01739，$\root{3}{x}$=17.39，$\root{3}{-5.26}$=y，求x和y的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．已知直角三角形的两直角边长分别是9cm和5cm，斜边长是xcm．
    （1）估计x在哪两个整数之间；
    （2）如果把x的结果精确到十分位，估计x的值在哪两个数之间，如果精确到百分位，用计算器验证你的估计值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．计算：
    （1）-13-（-15）+（-10）-9　              
    （2）$\frac{1}{2}$+（-$\frac{2}{3}$）+$\frac{4}{7}$+（-$\frac{1}{2}$）+（-$\frac{1}{3}$）
    （3）（-6.5）+（-2）÷（-$\frac{2}{5}$）÷（-5）
    （4）-14+[4-（$\frac{3}{8}$+$\frac{1}{6}$-$\frac{3}{4}$）×24]÷5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

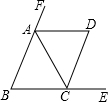    5．如图，在△ABC中，AB=AC，AD是△ABC外角的平分线，已知∠BAC=∠ACD．
    （1）求证：△ABC≌△CDA；
    （2）若∠B=60°，求证：四边形ABCD是菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．一物体从高2000米的飞机上自由落下，此物体高度h（米）和经过的时间之间的关系式为h=2000-4.9t2．
    （1）求此物体下落10秒时的高度；
    （2）此物体经过多少秒到达地面？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．填空：
    （1）已知DE∥BC，则△ADE∽△ABC；
    （2）已知∠A=∠D，则$\frac{CD}{AC}$=$\frac{CE}{BC}$=$\frac{DE}{AB}$（填边长比例关系）；
    （3）已知∠DAB=∠CAE，AB•AD=AE•AC，则∠ADE=∠C；
    （4）已知∠ABP=CDP，则PA•CD═PC•AB；
    （5）已知：∠ABC=90°，∠ACB=30°，AD=2AC，CD=2BC，则∠D=30°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．如图，已知△ABC．
    （1）请在图①上画出到△ABC的三个顶点距离相等的点P，这样点P有几个？
    （2）请在图②上画出到△ABC的三边距离相等的点M，这样的点M有几个？（不写作法，仅保留作图痕迹．）

    查看答案和解析>>

    科目：初中数学 来源：2017届内蒙古呼伦贝尔市海拉尔区九年级5月中考模拟考试数学试卷（解析版） 题型：判断题

    校车安全是近几年社会关注的重大问题，安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验：先在公路旁边选取一点C，再在笔直的车道l上确定点D，使CD与l垂直，测得CD的长等于21米，在l上点D的同侧取点A、B，使∠CAD＝30°，∠CBD＝60°.

    （1）求AB的长（精确到0.1米，参考数据：1.73，1.41）；

    （2）已知本路段对校车的限速为40千米/时，若测得某辆校车从A到B用时2秒，这辆校车是否超速？说明理由.

    查看答案和解析>>

    同步练习册答案