
【题目】如图,在四边形ABCD中,∠BAD=100°,∠B=∠D=90°,在BC、CD上分别找一个点M、N,使△AMN的周长最小,则∠AMN+∠ANM的度数为( )

A.130°B.120°C.160°D.100°
【答案】C
【解析】
要使△AMN的周长最小,即利用点的对称,使三角形的三边在同一直线上,作出A关于BC和CD的对称点A′,A″,即可得出∠AA′M+∠A″′=80°,进而得出∠AMN+∠ANM=2(∠AA′M+∠A″),即可得出答案.
解:作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值.
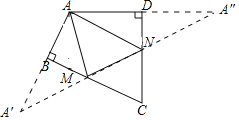
∵∠DAB=100°,
∴∠AA′M+∠A″=180°﹣∠BAD=180°﹣100°=80°,
∵∠MA′A=∠MAA′,∠NAD=∠A″,且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×80°=160°
故选:C.


科目:初中数学 来源: 题型:
【题目】已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为![]() 、
、![]() ,点D是OA的中点,点P在BC边上运动,当
,点D是OA的中点,点P在BC边上运动,当![]() 是等腰三角形时,点Р的坐标为_______________.
是等腰三角形时,点Р的坐标为_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知扇形![]() 中,
中,![]() ,弦
,弦![]() ,点
,点![]() 是弧
是弧![]() 上任意一点(与端点
上任意一点(与端点![]() 、
、![]() 不重合),
不重合),![]() 于点
于点![]() ,以点
,以点![]() 为圆心、
为圆心、![]() 长为半径作
长为半径作![]() ,分别过点
,分别过点![]() 、
、![]() 作
作![]() 的切线,两切线相交于点
的切线,两切线相交于点![]() .
.
![]() 求弧
求弧![]() 的长;
的长;
![]() 试判断
试判断![]() 的大小是否随点
的大小是否随点![]() 的运动而改变?若不变,请求出
的运动而改变?若不变,请求出![]() 的大小;若改变,请说明理由.
的大小;若改变,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为5的等边三角形,点D,E分别在BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的的延长线于点F,若BD=2,则DF等于( )
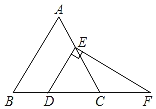
A.7B.6C.5D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=14,DE是线段AB的垂直平分线.
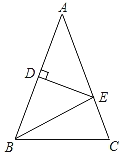
(1)若△EBC的周长是24,求BC的长;
(2)若∠A=x°,求∠EBC的度数(用含x的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列短文,回答有关问题:
在实数这章中,遇到过![]() 、
、![]() ;这样的式子,我们把这样的式子叫做二次根式,根号下的数叫做被开方数.如果一个二次根式的被开方数中有的因数能开的尽方,可以利用
;这样的式子,我们把这样的式子叫做二次根式,根号下的数叫做被开方数.如果一个二次根式的被开方数中有的因数能开的尽方,可以利用![]() 将这些因数开出来,从而将二次根式化简.当一个二次根式的被开方数中不含开得尽方的因数或者被开方数中不含有分数时,这样的二次根式叫做最简二次根式,例如,
将这些因数开出来,从而将二次根式化简.当一个二次根式的被开方数中不含开得尽方的因数或者被开方数中不含有分数时,这样的二次根式叫做最简二次根式,例如,![]() 化成最简二次根式是
化成最简二次根式是![]() ,
,![]() 化成最简二次根式是
化成最简二次根式是![]() .几个二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式叫做同类二次根式,如上面的例子就是同类二次根式.
.几个二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式叫做同类二次根式,如上面的例子就是同类二次根式.
![]() 请判断下列各式中,哪些是同类二次根式?
请判断下列各式中,哪些是同类二次根式?![]() ;
;
![]() 二次根式中的同类二次根式可以像整式中的同类项一样合并,请计算:
二次根式中的同类二次根式可以像整式中的同类项一样合并,请计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,AC的垂直平分线DE交AC于点D,交BC于点E,且∠BAE=90°,若DE=1,则BE=( )
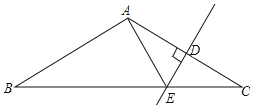
A.4B.3C.2D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1:5:6,③∠A=90°﹣∠B,④∠A=∠B=![]() ∠C中,能确定△ABC是直角三角形的条件有( )
∠C中,能确定△ABC是直角三角形的条件有( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李大妈加盟了“红红”全国烧烤连锁店,该公司的宗旨是“薄利多销”,经市场调查发现,当羊肉串的单价定为![]() 元时,每天能卖出
元时,每天能卖出![]() 串,在此基础上,每加价
串,在此基础上,每加价![]() 元李大妈每天就会少卖出
元李大妈每天就会少卖出![]() 串,考虑了所有因素后李大妈的每串羊肉串的成本价为
串,考虑了所有因素后李大妈的每串羊肉串的成本价为![]() 元,若李大妈每天销售这种羊肉串想获得利润是
元,若李大妈每天销售这种羊肉串想获得利润是![]() 元,那么请问这种羊肉串应怎样定价?
元,那么请问这种羊肉串应怎样定价?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com