
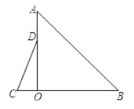
【题目】如图,在△AOB和△COD中,∠AOB=∠COD=90°,∠B=50°,∠C=60°,点D在边OA上,将图中的△COD绕点O按每秒20°的速度沿顺时针方向旋转一周,在旋转的过程中,在第t秒时,边CD恰好与边AB平行,则t的值为_______.
【答案】5.5或 14.5
【解析】
讨论:如图1,△COD绕点O顺时针旋转得到△C′OD′,C′D′交OB于E,根据平行线的判定,当∠OEC′=∠B=50°时,C′D′∥AB,则根据三角形外角性质计算出∠C′OC=110°,从而可计算出此时△COD绕点O顺时针旋转110°得到△C′OD′所需时间;如图2,△COD绕点O顺时针旋转得到△C″OD″,C″D″交直线OB于F,利用平行线的判定得当∠OFC″=∠B=50°时,C″D″∥AB,根据三角形内角和计算出∠C″OC=70°,则△COD绕点O顺时针旋290°得到△C″OD″,然后计算此时旋转的时间.
如图1,△COD绕点O顺时针旋转得到△C′OD′,C′D′交OB于E,则∠C′OD′=∠COD=90°,∠OC′D=∠C=60°,
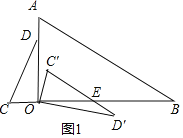
当∠OEC′=∠B=50°时,C′D′∥AB,
∴∠C′OC=∠OEC′+∠OC′E=50°+60°=110°,
∴△COD绕点O顺时针旋转110°得到△C′OD′所需时间为![]() =5.5(秒);
=5.5(秒);
如图2,△COD绕点O顺时针旋转得到△C″OD″,C″D″交直线OB于F,则∠C″OD″=∠COD=90°,∠OC″D″=∠C=60°,
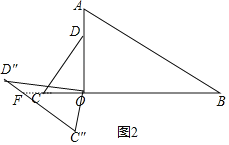
当∠OFC″=∠B=50°时,C″D″∥AB,
∴∠C″OC=180°-∠OFC″-∠OC″F=180°-50°-60°=70°,
而360°-70°=290°,
∴△COD绕点O顺时针旋290°得到△C″OD″所需时间为![]() =14.5(秒);
=14.5(秒);
综上所述,在旋转的过程中,在第5.5秒或14.5秒时,边CD恰好与边AB平行.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知,直线l1:y=3x﹣2k与直线l2:y=x+k交点P的纵坐标为5,直线l1与直线l2与y轴分别交于A、B两点.
(1)求出点P的横坐标及k的值;
(2)求△PAB的面积;
(3)点M为直线l1上的一个动点,当△MAB面积与△PAB面积之比为2:3时,求此时的点M的坐标【1】

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.
(1)求A,B两点的坐标;
(2)过B点作直线与x轴交于点P,若△ABP的面积为![]() ,试求点P的坐标.
,试求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格):
(1)画出△ABC中BC边上的高AD;
(2)画出先将△ABC向右平移6格,再向上平移3格后的△A1B1C1;
(3)画一个△BCP(要求各顶点在格点上,P不与A点重合),使其面积等于△ABC的面积.并回答,满足这样条件的点P共________个.

查看答案和解析>>
科目:初中数学 来源: 题型:
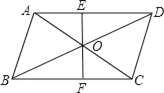
【题目】如图平行四边形ABCD中,对角线AC,BD交于点O,EF过点O,并与AD,BC分别交于点E,F,已知AE=3,BF=5
(1)求BC的长;
(2)如果两条对角线长的和是20,求三角形△AOD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.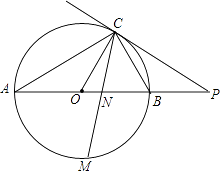
(1)求证:PC是⊙O的切线;
(2)求证:BC= ![]() AB;
AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=8,求MNMC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】5.1劳动节,某校决定组织甲乙两队参加义务劳动,并购买队服.下面是服装厂给出的服装的价格表:
购买服装的套数 |
|
|
|
每套服装的价格 |
|
|
|
经调查:两个队共75人(甲队人数不少于40人),如果分别各自购买队服,两队共需花费5600元,请回答以下问题:
(1)如果甲、乙两队联合起来购买服装,那么比各自购买服装最多可以节省_________.
(2)甲、乙两队各有多少名学生?
(3)到了现场,因工作分配需要,临时决定从甲队抽调a人,从乙队抽调b人,组成丙队(要求从每队抽调的人数不少于10人),现已知重新组队后,甲队平均每人需植树1棵;乙队平均每人需植树4棵;丙队平均每人需植树6棵,甲乙丙三队共需植树265棵,请写出所有的抽调方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC、直线l和格点O.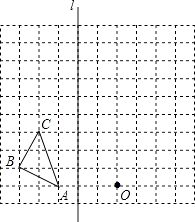
①画出△ABC关于直线l成轴对称的△A0B0C0;
②画出将△A0B0C0向上平移1个单位得到的△A1B1C1;
③以格点O为位似中心,将△A1B1C1作位似变换,将其放大到原来的两倍,得到△A2B2C2 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com