

| A. | ①>②>③ | B. | ③>②>① | C. | ②>③>① | D. | ①=②=③ |
分析 根据图①中直线的解析式找出直线与坐标轴的交点坐标,结合三角形的面积公式即可得出S的值;根据图②中反比例函数的解析式结合反比例函数系数k的几何意义即可得出S的值;根据图③中点的坐标利用待定系数法找出函数解析式,由此得出顶点坐标,再根据三角形的面积公式找出S的值.综上即可得出结论.
解答 解:①当x=0时,y=1;
当y=0时,x=1,
∴S=$\frac{1}{2}$×1×1=$\frac{1}{2}$;
②∵点在反比例函数y=$\frac{3}{x}$的图象上,
∴S=$\frac{1}{2}$k=$\frac{1}{2}$×3=$\frac{3}{2}$;
③由点(1,0)、(3,0)、(0,3)利用待定系数法求出抛物线解析式为y=x2-4x+3=(x-2)2-1,
∴抛物线的顶点坐标为(2,-1),
∴S=$\frac{1}{2}$×(3-1)×|-1|=1.
∵$\frac{1}{2}$<1<$\frac{3}{2}$,
∴②>③>①.
故选C.
点评 本题考查了抛物线与x轴的交点、一次函数图象上点的坐标特征以及反比例函数系数k的几何意义,根据三角形的面积公式求出3个图中阴影部分的面积是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{6}{9}$ | B. | $\frac{21}{56}$ | C. | $\frac{14}{18}$ | D. | $\frac{25}{30}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,小明家(A点)在一条河流(直线l,宽度忽略不计)的一侧,在河流的同侧有一公园(B点),小风家恰好关于此河流与小明家对称
如图,小明家(A点)在一条河流(直线l,宽度忽略不计)的一侧,在河流的同侧有一公园(B点),小风家恰好关于此河流与小明家对称查看答案和解析>>
科目:初中数学 来源: 题型:解答题
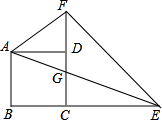 如图,已知正方形ABCD的边长为1,点E、F分别在边BC、CD的延长线上,AE与CD的交点为G,且∠EAF=45°.
如图,已知正方形ABCD的边长为1,点E、F分别在边BC、CD的延长线上,AE与CD的交点为G,且∠EAF=45°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
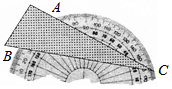 将一个三角形纸板按如图所示的方式放置一个破损的量角器上,使点C落在半圆上,若点A、B处的读数分别为65°、20°,则∠ACB的大小为22.5°.
将一个三角形纸板按如图所示的方式放置一个破损的量角器上,使点C落在半圆上,若点A、B处的读数分别为65°、20°,则∠ACB的大小为22.5°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com