
分析 观察原式的各项发现$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),利用此公式对各项进行变形,然后提取$\frac{1}{2}$,合并抵消后即可求出值.
解答 解:$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{99×101}$
=$\frac{1}{2}$×(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{99}$-$\frac{1}{101}$)
=$\frac{1}{2}$×(1-$\frac{1}{101}$)
=$\frac{1}{2}$×$\frac{99}{101}$
=$\frac{99}{202}$.
点评 此题考查了有理数的混合运算,利用的方法是裂项相消法,培养了学生的数感、符号感,灵活运用$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$)是解本题的关键.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
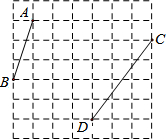 如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
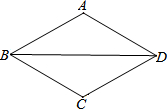 如图,△ABD≌△CBD,AB=AD,∠BAD=120°,点P从点B出发,沿线段BD向终点D运动,射线AP交折线B-C-D于点Q,当AP垂直△ABD的一腰时,PQ=2,则此时线段BP=4或8.
如图,△ABD≌△CBD,AB=AD,∠BAD=120°,点P从点B出发,沿线段BD向终点D运动,射线AP交折线B-C-D于点Q,当AP垂直△ABD的一腰时,PQ=2,则此时线段BP=4或8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知:如图,在△ABC与△DEC中,∠A=∠D,还需要添加两个条件才能使得△ABC≌△DEC,则错误的是( )
已知:如图,在△ABC与△DEC中,∠A=∠D,还需要添加两个条件才能使得△ABC≌△DEC,则错误的是( )| A. | AB=DE,∠B=∠E | B. | AB=DE,AC=DC | C. | BC=EC,∠BCE=∠ACD | D. | BC=EC,AC=DC |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com