
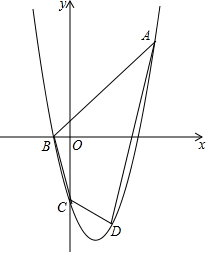
 如图,抛物线y=ax2+bx-4(a≠0)经过点A(5,6),与x轴的负半轴交于点B,与y轴交于点C,且OC=4OB.
如图,抛物线y=ax2+bx-4(a≠0)经过点A(5,6),与x轴的负半轴交于点B,与y轴交于点C,且OC=4OB.分析 (1)可先求得C点坐标,则可求得OB长,可求得B点坐标,再把A、B坐标代入可求得抛物线解析式;
(2)由点D在第四象限,当△ABD为直角三角形时有∠DBA=90°或∠BDA=90°,①当∠DBA=90°时,过D作DE⊥x轴于点E,则可知DE=BE,可得到关于D点坐标的方程,可求得D点坐标,②当∠BDA=90°时,过D作DF⊥x轴于点F,过A作AG⊥x轴于点G,过在作DH∥x轴,交AG于点H,则可得到∠DBF=∠DHA,利用三角形相似可得到关于D点坐标的方程,可求得D点坐标.
解答 解:
(1)在y=ax2+bx-4中,令x=0可得y=-4,
∴C(0,-4),
∴OC=4,
∴OB=1,
∴B(-1,0),
把A、B坐标代入抛物线解析式可得$\left\{\begin{array}{l}{a-b-4=0}\\{25a+5b-4=6}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=1}\\{b=-3}\end{array}\right.$,
∴抛物线解析式为y=x2-3x-4;
(2)∵点D在第四象限的抛物线上,
∴可设D(x,x2-3x-4)(x>0且x2-3x-4<0),
当△ABD为直角三角形时,则只有∠DBA=90°或∠BDA=90°,
①当∠DBA=90°时,过D作DE⊥x轴于点E,如图1,
∵B(-1,0),A(5,6),
∴直线AB解析式为y=x+1,
∴∠ABO=45°,
∴∠EBD=45°,
∴DE=BE,
∵B(-1,0),D(x,x2-3x-4),
∴BE=x+1,DE=-x2+3x+4,
∴x+1=-x2+3x+4,解得x=-1或x=3,
当x=-1时,B、D重合,舍去,当x=3时,x2-3x-4=-4,
∴D(3,-4);
②当∠BDA=90°时,过D作DF⊥x轴于点F,过A作AG⊥x轴于点G,过在作DH∥x轴,交AG于点H,如图2,
∵∠DBF+∠BDA=∠AGF+∠FAG,
∴∠DBF=∠DHA,
∴△BDF∽△ADH,
∴$\frac{DF}{BF}$=$\frac{DH}{AH}$,即$\frac{-{x}^{2}+3x+4}{x+1}$=$\frac{6-(x+1)}{6-({x}^{2}-3x-4)}$,解得x=1+2$\sqrt{2}$或x=1-2$\sqrt{2}$(小于0,舍去),此时x2-3x-4=2-2$\sqrt{2}$,
∴D(1+2$\sqrt{2}$,2-2$\sqrt{2}$),
综上可知D点坐标为(3,-4)或(1+2$\sqrt{2}$,2-2$\sqrt{2}$).
点评 本题为二次函数的综合应用,涉及待定系数法、直角三角形的性质、相似三角形的判定和性质、方程思想及分类讨论思想等知识.在(1)中求得A点坐标是解题的关键,在(2)中确定出D点的位置,得到关于D点坐标的方程是解题的关键.本题考查知识点较多,综合性很强,难度适中.


科目:初中数学 来源: 题型:解答题
| 与标准质量的差值(单位:克) | -5 | -2 | 0 | 1 | 3 | 4 |
| 袋数 | 2 | 4 | 5 | 4 | 3 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 电信部门要在P区域内修建一座电视信号发射塔.如图,按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条高速公路m和n的距离也必须相等.发射塔应修建在什么位置?在图中标出它的位置.(要求:尺规作图,不写作法,但要保留作图痕迹,并写出结论)
电信部门要在P区域内修建一座电视信号发射塔.如图,按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条高速公路m和n的距离也必须相等.发射塔应修建在什么位置?在图中标出它的位置.(要求:尺规作图,不写作法,但要保留作图痕迹,并写出结论)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是$\widehat{EB}$的中点,则下列结论:①OC∥AE;②EC=BC;③∠DAE=∠ABE;④AC⊥OE,其中正确的有( )
如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是$\widehat{EB}$的中点,则下列结论:①OC∥AE;②EC=BC;③∠DAE=∠ABE;④AC⊥OE,其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com