
 如图,在△ABC中,∠ABC,∠ACB的平分线交于点O,D是∠ACB外角与内角∠ABC平分线交点,E是∠ABC,∠ACB外角平分线交点,若∠BOC=120°,则∠D=( )度.
如图,在△ABC中,∠ABC,∠ACB的平分线交于点O,D是∠ACB外角与内角∠ABC平分线交点,E是∠ABC,∠ACB外角平分线交点,若∠BOC=120°,则∠D=( )度.| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
分析 根据角平分线的定义有∠ABC=2∠OBC,∠ACB=2∠0CB,根据三角形内角和定理得2∠OBC+2∠OCB+∠A=180°,即有∠OCB+∠OBC=90°-$\frac{1}{2}$∠A,再根据三角形内角和定理得到∠OCB+∠OBC+∠BOC=180°,于是有∠BOC=90°+$\frac{1}{2}$∠A,即可得到∠BOC的度数,三角形外角的性质有∠FCD=∠D+∠DBC,∠ACF=∠ABC+∠A,则2∠D+2∠DBC=∠ABC+∠A,即可得到∠D=$\frac{1}{2}$∠A,于是得到∠D,然后根据三角形的内角和即可得到结论.
解答  解:∵BO平分∠ABC,CO平分∠ACB,
解:∵BO平分∠ABC,CO平分∠ACB,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
又∵∠ABC+∠ACB+∠A=180°,
∴2∠OCB+2∠OBC+∠A=180°,
∴∠OCB+∠OBC=90°-$\frac{1}{2}$∠A,
又∵∠OCB+∠OBC+∠BOC=180°,
∴90°-$\frac{1}{2}$∠A+∠BOC=180°,
∴∠BOC=90°+$\frac{1}{2}$∠A,
而∠BOC=120°,
∴∠A=60°,
∵∠DCF=∠D+∠DBC,∠ACF=∠ABC+∠A,BD平分∠ABC,DC平分∠ACF,
∴∠ACF=2∠DCF,∠ABC=2∠DBC,
∴2∠D+2∠DBC=∠ABC+∠A,
∴2∠D=∠A,即∠D=$\frac{1}{2}$∠A.
∵∠A=60°,
∴∠D=30°,
故选D.
点评 本题考查了角平分线定义,三角形内角和定理的应用,熟知三角形的内角和等于180°是解答此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{{2{x^2}}}{x}$ | B. | a+b | C. | $\frac{1}{2x+1}$ | D. | $\frac{2x-2}{x-1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 40°50′=40.5° | |
| B. | 若线段AP=BP,则P一定是AB中点 | |
| C. | 若∠AOC=$\frac{1}{2}$∠AOB,则OC是∠AOB的平分线 | |
| D. | 连结两点的线段的长度叫做两点之间的距离 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,以数轴的单位长度线段为边作一个正方形,以表示数-2的点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A表示的数是( )
如图,以数轴的单位长度线段为边作一个正方形,以表示数-2的点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A表示的数是( )| A. | -$\sqrt{2}$ | B. | -2+$\sqrt{2}$ | C. | -2-$\sqrt{2}$ | D. | 1-$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,点O是坐标原点,A(0,6),AB=4$\sqrt{3}$,且∠OBA=60°,将△OAB沿直线AB翻折,得到△CAB,点O与点C对应.
如图,在平面直角坐标系中,点O是坐标原点,A(0,6),AB=4$\sqrt{3}$,且∠OBA=60°,将△OAB沿直线AB翻折,得到△CAB,点O与点C对应.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
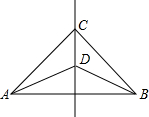 CD是线段AB的垂直平分线,则∠CAD=∠CBD.请说明理由.
CD是线段AB的垂直平分线,则∠CAD=∠CBD.请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com