
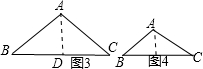
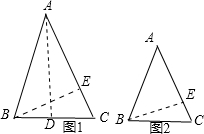
 解:如图1、2,当30°内角为顶角时,
解:如图1、2,当30°内角为顶角时,| 1 |
| 2 |
| 1 |
| 2 |
| λ2-1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| λ2-1 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 6 |
| 2 |
| 6 |
| 2 |
| 3 |
| 3 |
| ||
| 3 |
4
| ||
| 3 |
| 2 |
| 6 |
| 2 |
| 3 |
4
| ||
| 3 |


科目:初中数学 来源: 题型:
| 5 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 为了解2012年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况,随机调查了部分参赛同学的成绩,整理并制作图表如下.请根据以上图表提供的信息,解答下列问题:
为了解2012年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况,随机调查了部分参赛同学的成绩,整理并制作图表如下.请根据以上图表提供的信息,解答下列问题:| 分数段 | 频数 | 频率 |
| 自然科学 | 400 | 0.20 |
| 文艺艺术 | 1000 | 0.5 |
| 社会百科 | 500 | 0.25 |
| 数学 | m | n |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,矩形ABCD中,E为对角线BD上一点,连接AE交CD于G,交BC延长线于F,∠DAE=∠DCE,∠AEB=∠CEB.
如图,矩形ABCD中,E为对角线BD上一点,连接AE交CD于G,交BC延长线于F,∠DAE=∠DCE,∠AEB=∠CEB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com