
分析 (1)先把方程化为一般形式:3x2+10x+5=0,然后把a=3,b=10,c=5代入求根公式计算即可.
(2)进而提取公因式(x-2)分解因式得出即可.
(3)首先将常数项移到等号的右侧,将等号左右两边同时加上一次项系数一半的平方,即可将等号左边的代数式写成完全平方形式.
(4)方程变形后,利用平方差公式分解,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.
解答 解:(1)方程化为一般形式,得2x2-3x-3=0,
∵a=2,b=-3,c=-3,
∴b2-4ac=(-3)2-4×2×(-3)=33>0,
∴x=$\frac{3±\sqrt{33}}{2×2}$=$\frac{3±\sqrt{33}}{4}$,
∴x1=$\frac{{3+\sqrt{33}}}{4}$,x2=$\frac{{3-\sqrt{33}}}{4}$;
(2)3(x-2)2=x(x-2)
3(x-2)2-x(x-2)=0
(x-2)(3x-6-x)=0,
∴x-2=0,2x-6=0,
∴x1=2,x2=3;
(3)x1=$\frac{{5+\sqrt{21}}}{2}$,x2=$\frac{{5-\sqrt{21}}}{2}$
(4)方程变形得:(y+2)2-(3y-1)2=0,
分解因式得:(y+2+3y-1)(y+2-3y+1)=0,
∴4y+1=0或-2y+3=0,
∴y1=$\frac{3}{2}$,y2=$-\frac{1}{4}$.
点评 本题考查了解一元二次方程,熟练掌握解一元二次方程的方法是解题的关键.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
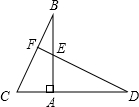 如图,已知Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转,使点D落在射线CA上,DE的延长线交BC于F,则∠CFD的度数为( )
如图,已知Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转,使点D落在射线CA上,DE的延长线交BC于F,则∠CFD的度数为( )| A. | 80° | B. | 90° | C. | 100° | D. | 120° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com