
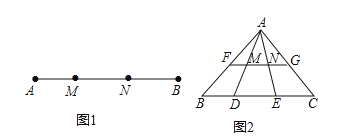
【题目】定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.
请解决下列问题:
(1)已知点M,N是线段AB的勾股分割点,且BN>MN>AM.若AM=2,MN=3,求BN的长;
(2)如图2,若点F、M、N、G分别是AB、AD、AE、AC边上的中点,点D,E是线段BC的勾股分割点,且EC>DE>BD,求证:点M,N是线段FG的勾股分割点.
【答案】(1)![]() (2)证明见解析.
(2)证明见解析.
【解析】试题分析:(1)①当MN为最大线段时,由勾股定理求出BN;②当BN为最大线段时,由勾股定理求出BN即可;
(2)先证出点M、N分别是AD、AE的中点,得出BD=2FM,DE=2MN,EC=2NG,求出EC2=BD2+DE2,得出NG2=FM2+MN2,即可得出结论
试题解析:(1)∵点M,N是线段AB的勾股分割点,且BN>MN>AM, AM=2,MN=3
∴![]()
![]()
∴BN=![]()
(2)证明 ∵点F、M、N、G分别是AB、AD、AE、AC边上的中点
∴FM、MN、NG分别是△ABD、△ADE、△AEC的中位线
∴BD=2FM,DE=2MN,EC=2NG
∵点D,E是线段BC的勾股分割点,且EC>DE>BD
∴![]()
∴![]()
∴![]()
∴点M,N是线段FG的勾股分割点


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】将7张如图①所示的长为a、宽为b(a>b)的小长方形纸片,按如图②所示的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示,设左上角与右下角的阴影部分的面积之差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a、b应满足( )
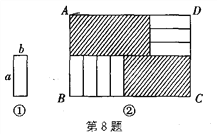
A. a=![]() b B. a=3b C. a=
b B. a=3b C. a=![]() b D. a=4b
b D. a=4b
查看答案和解析>>
科目:初中数学 来源: 题型:
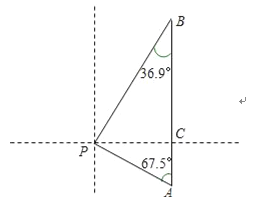
【题目】如图某天上午9时,向阳号轮船位于A处,观测到某港口城市P位于轮船的北偏西67.5°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到城市P位于该船的南偏西36.9°方向,求此时轮船所处位置B与城市P的距离?(参考数据:sin36.9°≈![]() ,tan36.9°≈
,tan36.9°≈![]() ,sin67.5°≈
,sin67.5°≈![]() ,tan67.5°≈
,tan67.5°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8 …,顶点依次为A1,A2,A3,A4,A5,…,则顶点A55的坐标是( )
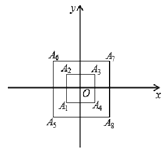
A. (13,13) B. (-13,-13) C. (-14,-14) D. (14,14)
查看答案和解析>>
科目:初中数学 来源: 题型:
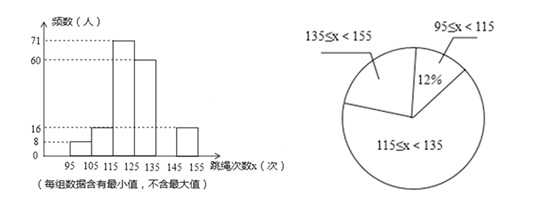
【题目】在我县开展的“阳光体育”跳绳活动中,为了了解初中学生跳绳活动的开展情况,随机抽查了全县七年级部分同学1分钟跳绳的次数,将抽查结果进行统计,并绘制两个不完整的统计图.请根据图中提供的信息,解答下列问题:
(1)本次共抽查了多少名学生?
(2)请补全频数分布直方图空缺部分,直接写出扇形统计图中跳绳次数范围135≤x<155所在扇形的圆心角度数;
(3)若本次抽查中,跳绳次数在125次以上(含125次)为优秀,请你估计全县8000名初中学生中有多少名学生的成绩为优秀?
(4)请你根据以上信息,对我市开展的学生跳绳活动谈谈自己的看法或建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
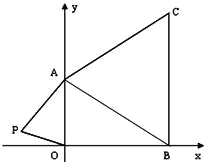
【题目】如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式![]()
(1)求a、b、c的值;
(2)如果在第二象限内有一点P(m, ![]() ),请用含m的式子表示四边形ABOP的面积;
),请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积为△ABC的面积相等?若存在,求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com