
| A. | 10、91 | B. | 12、91 | C. | 10、95 | D. | 12、95 |
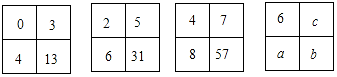
分析 分析前三个正方形,发现“右上的数=左上的数+3,左下的数=左上的数+4,右下的数=右上的数×右下的数+1”,依此即可得出a、b、c的值.
解答 解:分析正方形中的四个数:
∵第一个正方形中0+3=3,0+4=4,3×4+1=13;第二个正方形中2+3=5,2+4=6,5×6+1=31;第三个正方形中4+3=7,4+4=8,7×8+1=57.
∴c=6+3=9,a=6+4=10,c=9×10+1=91.
故选A.
点评 本题考查了规律型中的数字的变换类,解题的关键是分析正方形中四个数找出它们之间的关系“右上的数=左上的数+3,左下的数=左上的数+4,右下的数=右上的数×右下的数+1”.本题属于基础题,难度不大,解决该题型题目时,根据给定的正方形中的4个数,找出它们之间的关系是关键.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 填写下面证明过程中的推理依据:
填写下面证明过程中的推理依据:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星 期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增 减 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 100元 | B. | 200元 | C. | 300元 | D. | 400元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com