
 如图,已知?ABCD中,AE⊥BC,点E是垂足,AE与BD交于点G,且DG=2AB,∠DBC=25°.求∠ABD的度数.
如图,已知?ABCD中,AE⊥BC,点E是垂足,AE与BD交于点G,且DG=2AB,∠DBC=25°.求∠ABD的度数. 分析 首先取DG的中点F,连接AF,由?ABCD中,AE⊥BC,根据直角三角形斜边的中线等于斜边的一半,可得AF=DF,又由∠DBC=25°,根据等边对等角的性质,可求得∠DAF的度数,继而求得∠AFB的度数,然后由DG=2AB,证得AB=AF,则可求得答案.
解答  解:取DG的中点F,连接AF,
解:取DG的中点F,连接AF,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADF=∠DBC=25°,
∵AE⊥BC,
∴AE⊥AD,
即∠GAD=90°,
∴AF=DF=$\frac{1}{2}$DG,
∴∠DAF=∠ADF=25°,
∴∠AFB=∠DAF+∠ADF=50°,
∵DG=2AB,
∴AF=AB,
∴∠ABD=∠AFB=50°.
点评 此题考查了平行四边形的性质、等腰三角形的判定与性质以及直角三角形斜边上的中线的性质.注意准确作出辅助线是解此题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
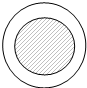 如图所示,航空兵一定能把物资投到指定的区域(大圆)内,但落在中心区域小圆(阴影部分)的概率为$\frac{1}{2}$,则小圆与大圆半径之比为$\frac{\sqrt{2}}{2}$.
如图所示,航空兵一定能把物资投到指定的区域(大圆)内,但落在中心区域小圆(阴影部分)的概率为$\frac{1}{2}$,则小圆与大圆半径之比为$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC为等腰直角三角形,其中BC长为10.
如图,△ABC为等腰直角三角形,其中BC长为10.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com